题目内容
【题目】如图,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,若四边形ABCD的面积是24cm2,求AC的长
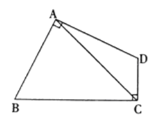
【答案】4![]()
【解析】
过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F,利用三个角为直角的四边形为矩形得到AECF为矩形,利用矩形得四个角为直角得到∠EAF为直角,利用等式的性质得到∠DAF=∠BAE,再由一对直角相等,AB=AD,利用AAS得到三角形ABE与三角形ADF全等,利用全等三角形的对应边相等得到AE=AF,可得出AECF为正方形,三角形ABE面积与三角形AFD面积相等,进而得到四边形ABCD面积等于正方形AECF面积,求出正方形的边长即为AE的长,在等腰直角三角形ACE中,利用勾股定理即可求出AC的长.
解:过A作AE⊥BC,作AF⊥CD,交CD的延长线于点F,
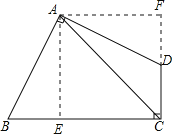
∵∠AEC=∠AFC=∠ECF=90°,
∴四边形AECF为矩形,
∴∠EAF=90°,
∵∠BAD=90°,
∴∠BAE+∠EAD=∠FAD+∠EAD=90°,
∴∠DAF=∠BAE,
在△ABE和△ADF中,
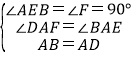
∴△ABE≌△ADF(AAS),
∴AE=AF,S△ABE=S△ADF,
∴四边形AECF是正方形,
∴S四边形ABCD=S正方形AECF=24cm2,
∴AE=2![]() cm,
cm,
∵△AEC为等腰直角三角形,
∴AC=![]() AE=4
AE=4![]() cm.
cm.
故答案为:4![]() .
.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目