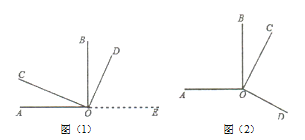��Ŀ����
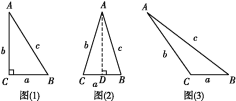
����Ŀ����ͼ1������ABCD�У���֪��BAD=120�㣬��EGF=60�㣬��EGF�Ķ���G�����ζԽ���AC���˶����ǵ����߷ֱ�BC��CD�ڵ�E��F��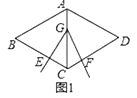
��1����ͼ2��������G�˶������A�غ�ʱ����֤��EC+CF=BC��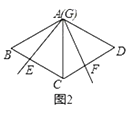
��2��֪ʶ̽��������ͼ3��������G�˶���AC�е�ʱ��̽���߶�EC��CF��BC��������ϵ��
���ڶ���G���˶������У��� ![]() =t����ֱ��д���߶�EC��CF��BC��������ϵ������Ҫд��֤�����̣���
=t����ֱ��д���߶�EC��CF��BC��������ϵ������Ҫд��֤�����̣���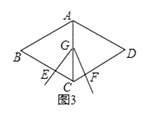
��3������������ͼ4����֪���α߳�Ϊ8��BG=7��CF= ![]() ����t��2ʱ����EC�ij��ȣ�
����t��2ʱ����EC�ij��ȣ�
���𰸡�
��1��֤������ͼ2�У���CA��ȡһ��M��ʹ��CM=CE������EM��
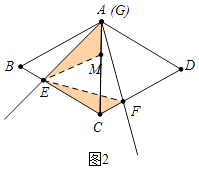
���ı���ABCD�����Σ���BAD=120�㣬
��AB=BC=CD=AD����CAB=��CAD=60�㣬
���ABC����ACD���ǵȱ������Σ�
���AB=AC����BAC=��EAF=60�㣬��B=��ACF=60�㣬
���BAE=��CAF��
�ڡ�BAE�͡�CAF�У� 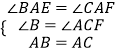 ��
��
���ABE�ա�ACF��
��AE=AF���ߡ�EAF=60�㣬
���AEF�ǵȱ������Σ�
��CE=CM����ECM=60�㣬
���ECM�ǵȱ������Σ�
���AEF=��MEC=60�㣬AE=EF��EM=EC��
���AEM=��FEC��
�ڡ�AEM�͡�FEC�У�
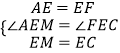 ��
��
���AEM�ա�FEC��
��AM=CF��
��BC=AC=AM+CM=EC+CF
��2���⣺�ٽ��ۣ�EC+CF= ![]() BC��
BC��
���ɣ���ͼ3�У�ȡBC�е�P��CD�е�Q������PG��GQ��
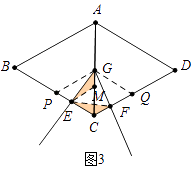
��AG=GC��CPB��CQ=DQ��
��PG��AB��GQ��QD��
���CPG=��B=60�㣬��CGP=��CAB=60�㣬
���CPG�ǵȱ������Σ�ͬ����֤��CQG�ǵȱ������Σ�
�ɣ�1����֪��CE+CF=PC= ![]() BC��
BC��
�ڽ��ۣ�CE+CF= ![]() ��
��
���ɣ���ͼ4�У���GP��AB��BC��P��GQ��AD��CD��Q��
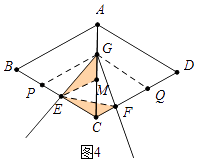
��PG��AB��GQ��QD��
���CPG=��B=60�㣬��CGP=��CAB=60�㣬
���CPG�ǵȱ������Σ�ͬ����֤��CQG�ǵȱ������Σ�
�ɣ�1����֪��CE+CF=PC=CG��
��AC=BC=tCG��
��CE+CF= ![]()
��3����ͼ4�У���BM��AC��M��
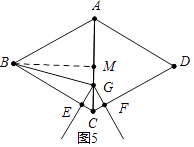
��t��2��
���G���߶�CM�ϣ�
��Rt��ABM�У��ߡ�BMC=90�㣬BM= ![]() ��8=4
��8=4 ![]() ��BG=7��
��BG=7��
��MG= ![]() =
= ![]() =1��
=1��
��CM=MA=4��
��CG=CM��MG=3��
�ɣ�1����֪��CG=CE+CF��
��CE=CG��CF=3�� ![]() =
= ![]()
����������1����ͼ2�У���CA��ȡһ��M��ʹ��CM=CE������EM������֤����ABE�ա�ACF����֤����AEM�ա�FEC�����ɽ�����⣮��2���ٽ��ۣ�EC+CF= ![]() BC����ͼ3�У�ȡBC�е�P��CD�е�Q������PG��GQ�����ã�1���Ľ��۽�����⣮�ڽ��ۣ�CE+CF=
BC����ͼ3�У�ȡBC�е�P��CD�е�Q������PG��GQ�����ã�1���Ľ��۽�����⣮�ڽ��ۣ�CE+CF= ![]() ����ͼ4�У���GP��AB��BC��P��GQ��AD��CD��Q�����ã�1���Ľ��۽�����⣮��3����ͼ4�У���BM��AC��M�����ã�1���Ľ��ۣ�CG=CE+CF�����CE���ɽ�����⣮
����ͼ4�У���GP��AB��BC��P��GQ��AD��CD��Q�����ã�1���Ľ��۽�����⣮��3����ͼ4�У���BM��AC��M�����ã�1���Ľ��ۣ�CG=CE+CF�����CE���ɽ�����⣮
�����㾫��������ȫ�������ε����ʺ����ε������ǽ����ĸ�������Ҫ֪��ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ����ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮

����Ŀ����ͼ��BCΪ��Բ��ֱ����OΪԲ�ģ�D�ǻ�AC���е㣬�ı���ABCD�ĶԽ���AC��BD���ڵ�E��BC= ![]() ��CD=
��CD= ![]() ����sin��AEB��ֵΪ ��
����sin��AEB��ֵΪ �� 
����Ŀ��ij��ͯ������Ʊ�۸�涨���±���
��Ʊ���� | 1��50�� | 51��100�� | 100������ |
ÿ��Ʊ�ļ۸� | 13Ԫ | 11Ԫ | 9Ԫ |
ijУ���꼶��1������2�������102�˽���6.1��ͯ��ȥ�θ����������У�1�����������٣�����50�ˡ������㣬����������Ϊ��λ��Ʊ����һ��Ӧ��1218Ԫ���ʣ�
��1����������ж���ѧ����
��2���������������������Ϊһ�����幺Ʊ�����Խ�ʡ����Ǯ��