题目内容
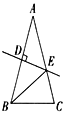
【题目】如图,点A,B,C在同一直线上,△ABD和△BCE都是等边三角形,AE,CD分别与BD,BE交于点F,G,连接FG,有如下结论:①AE=CD ②∠BFG= 60°;③EF=CG;④AD⊥CD⑤FG ∥AC 其中,正确的结论有__________________. (填序号)

【答案】①②③⑤
【解析】
易证△ABE≌△DBC,则有∠BAE=∠BDC,AE=CD,从而可证到△ABF≌△DBG,则有AF=DG,BF=BG,由∠FBG=60°可得△BFG是等边三角形,证得∠BFG=∠DBA=60°,则有FG∥AC,由∠CDB≠30°,可判断AD与CD的位置关系.
∵△ABD和△BCE都是等边三角形,∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°.
∵点A、B、C在同一直线上,∴∠DBE=180°﹣60°﹣60°=60°,∴∠ABE=∠DBC=120°.
在△ABE和△DBC中,∵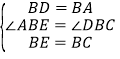 ,∴△ABE≌△DBC,∴∠BAE=∠BDC,∴AE=CD,∴①正确;
,∴△ABE≌△DBC,∴∠BAE=∠BDC,∴AE=CD,∴①正确;
在△ABF和△DBG中,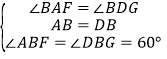 ,∴△ABF≌△DBG,∴AF=DG,BF=BG.
,∴△ABF≌△DBG,∴AF=DG,BF=BG.
∵∠FBG=180°﹣60°﹣60°=60°,∴△BFG是等边三角形,∴∠BFG=60°,∴②正确;
∵AE=CD,AF=DG,∴EF=CG;∴③正确;
∵∠ADB=60°,而∠CDB=∠EAB≠30°,∴AD与CD不一定垂直,∴④错误.
∵△BFG是等边三角形,∴∠BFG=60°,∴∠GFB=∠DBA=60°,∴FG∥AB,∴⑤正确.
故答案为:①②③⑤.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目