题目内容
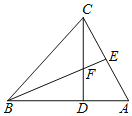
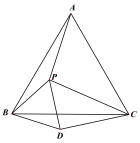
【题目】已知:如图,点P是等边△ABC内的一点,连接PA、PB、PC,以PB为边作等边△BPD,连接CD,若∠APB=150°,BD=6,CD=8,△APB的面积为( ).
A.48B.24C.12D.10
【答案】C
【解析】
作CM⊥BD交BD的延长线于M,利用全等三角形的性质证明∠BDC=150°,解直角三角形求出CM即可解决问题;
解:作CM⊥BD交BD的延长线于M,

∵∠ABC=∠PBD=60°,
∴∠ABP=∠CBD,
∵△ABC和△BPD是等边三角形,
∴AB=BC,BP=BD,
在△ABP和△CBD中,
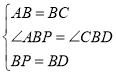 ,
,
∴△ABP≌△CBD(SAS),
∴∠CDB=∠APB=150°,
∴∠CDM=30°,∠M=90°,
∴![]() ,
,
∴![]() ,
,
又△ABP≌△CBD,
∴△APB的面积为12,
故选C.

练习册系列答案
相关题目
【题目】九(1)班组织班级联欢会,最后进入抽奖环节,每名同学都有一次抽奖机会,抽奖方案如下:将一副扑克牌中点数为“2”,“3”,“3”, “5”,“6”的四张牌背面朝上洗匀,先从中抽出1张牌,再从余下的4张牌中抽出1张牌,记录两张牌点数后放回,完成一次抽奖,记每次抽出两张牌点数之差为x,按表格要求确定奖项.
奖项 | 一等奖 | 二等奖 | 三等奖 |
|x| | |x|=4 | |x|=3 | 1 |
(1)用列表或画树状图的方法求出甲同学获得一等奖的概率;
(2)求出每次抽奖获奖的概率?