Question

【题目】已知，△ABC中，∠ACB＝90°，AC＝BC，以AC为边在同一平面内作等边△ACD，连接BD，则∠ADB＝______________．

Answer 1

【答案】45°或135°

【解析】

根据等边三角形的性质得出DC=BC，进而得出∠CDB=15°解答即可．

解：如图：

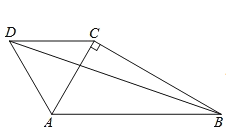
∵△ACD是等边三角形，

∴DC=AC=AD，∠DCA=∠ADC=60°，

∵AC=BC，

∴DC=BC，

∴∠CDB=，

∴∠ADB=，

如图，当D在AC的右侧时，△ACD是等边三角形，

∴∠ADC=60°，∠ACD=60°，CD=AC，

∵∠ACB=90°，

∴∠DCB=90°-60°=30°，

∵AC=BC，

∴CD=BC，

∴，

则∠ADB=∠ADC+∠CDB=60°+75°=135°；

故答案为：45°或135°.