题目内容
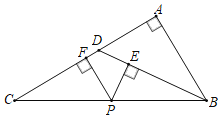
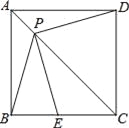
【题目】如图,AD⊥BC于D,BE⊥AC于F,BE交AD于F,BF=AC,
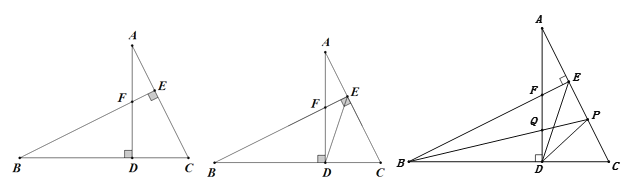
(1)求证:FD=CD;
(2)连DE,求证:ED平分∠BEC;
(3)在(2)条件下,点P在AC上,连BP、DP,BP交AD于Q, BP平分∠EBC,∠BPD=![]() ∠BFD,△APQ的面积为4,求线段PD的长.
∠BFD,△APQ的面积为4,求线段PD的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() ;
;
【解析】
(1)先证明△BFD![]() △ACD,即可得出FD=CD;
△ACD,即可得出FD=CD;
(2)过D作DG⊥BE于G,DH⊥AC于H,由“AAS”可证△BDG![]() △ADH,可得DG=DH,由角平分线的性质可得ED平分∠BEC;
△ADH,可得DG=DH,由角平分线的性质可得ED平分∠BEC;
(3)如图,过点P作PH⊥CD于H,PN⊥AD于N,延长PN交BE于点G,由角平分线的性质可证PH=PN=PE,通过全等三角形的性质可证AE=PE=PH,由面积公式可得PH=2,由直角三角形的性质可求解;
(1)证明:∵AD⊥BC于D,BE⊥AC于F,
∴∠BDA=∠CDA=90°,∠FEA=90°,
∵∠BFD=∠AFE,∠BFD+∠FBD=90°,∠AFE+∠FAE=90°,
∴∠FBD=∠FAE=∠CAD,
∵∠DAC+∠ACD=90°,∠BFD=∠AFE,∠AFE+∠FAE=90°,
∴∠BFD=∠ACD,
在△BFD和△ACD中,
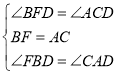
∴△BFD![]() △ACD,
△ACD,
∴FD=CD;
(2)证明:如图1,过D作DG⊥BE于G,DH⊥AC于H,
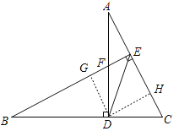
∵△BFD![]() △ACD,
△ACD,
∴∠B=∠A,BD=AD,
∴△BDG![]() △ADH,
△ADH,
∴DG=DH,且DG⊥BE,DH⊥AC,
∴ED平分∠BEC;
(3)如图,过点P作PH⊥CD于H,PN⊥AD于N,延长PN交BE于点G,
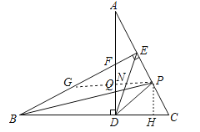
∵BP平分∠EBC,PH⊥BC,∠PEB=90°,PE=PH,
∴∠EBP=∠PBD,
∵∠PDC=∠PBD+∠BPD=![]() ,
,
∴∠PDC=![]() =45°,且∠ADC=90°,
=45°,且∠ADC=90°,
∴∠ADP=∠PDC=45°,且PH⊥DC,PN⊥AD,
∴PH=PN,
∴PH=PN=PE,且∠APN=∠GPE,∠ANP=∠GEP=90°,
∴△APN![]() △GPE,
△GPE,
∴AP=GP,
∴AE=GQ,
∵PH⊥CD,PN⊥AD,AD⊥CB,
∴四边形DHPN是矩形,且PH=PN,
∴四边形DHPN是正方形,
∴PH=QD=DH=NP,且FD=CD,
∴FN=CH,
∵∠A+∠C=90°,∠A+∠AFE=90°
∴∠C=∠AFE=∠GFN,且FN=CH,∠PHC=∠GNF,
∴△GNF![]() △PHC,
△PHC,
∴PH=GN,
∴PH=AE=PE,
∵∠APB=∠PBC+∠C,∠AQP=∠GFN+∠EBP,
∴∠APB=∠AQP,
∴AP=AQ=2PH,
∵△APQ的面积为4,
∴![]() ,
,
∴![]() ,
,
∴PH=2,
∴PH=DH=2,且PH⊥CD,
∴![]() ;
;

 阅读快车系列答案
阅读快车系列答案