题目内容
【题目】综合与探究
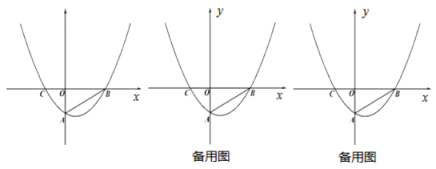
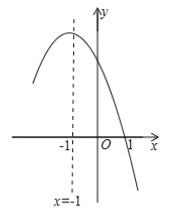
如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() 点
点![]() 是
是![]() 的平分线与抛物线的交点.
的平分线与抛物线的交点.
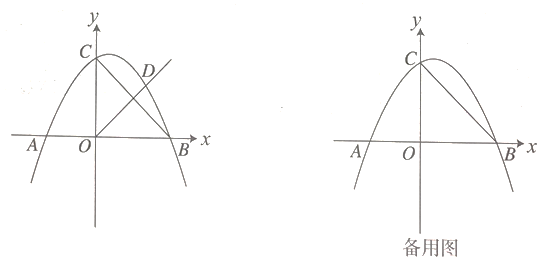
![]() 求抛物线的解析式及点
求抛物线的解析式及点![]() 的坐标;
的坐标;
![]() 点
点![]() 在平面直角坐标系内,且以
在平面直角坐标系内,且以![]() 点为顶点的四边形是平行四边形,请直接写出满足条件的点
点为顶点的四边形是平行四边形,请直接写出满足条件的点![]() 的坐标.
的坐标.
![]() 若点
若点![]() 是直线
是直线![]() 上方抛物线上的一个动点,且点
上方抛物线上的一个动点,且点![]() 的横坐标为
的横坐标为![]() 请写出
请写出![]() 的面积
的面积![]() 与
与![]() 之间的关系式,并求出
之间的关系式,并求出![]() 为何值时,
为何值时,![]() 的面积
的面积![]() 有最大值,最大值为多少.
有最大值,最大值为多少.
【答案】(1) ![]() ,
,![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]()
【解析】
(1)根据![]() ,可得
,可得![]() ,再利用待定系数法即可求得
,再利用待定系数法即可求得![]() ,再根据点
,再根据点![]() 是
是![]() 的平分线与抛物线的交点,可设
的平分线与抛物线的交点,可设![]() ,代入抛物线
,代入抛物线![]() ,即可求解.
,即可求解.
(2)分以OB、OD为邻边的平行四边形、以OB、BD为邻边的平行四边形、以DB、OD为邻边的平行四边形三种情况 .
(3)作直线![]() 轴于点
轴于点![]() 交
交![]() 于点
于点![]() ,
,![]() 点坐标为
点坐标为![]() ,设直线
,设直线![]() 的解析式
的解析式![]() ,根据
,根据![]() ,可得直线
,可得直线![]() 解析式为
解析式为![]()
![]() ,
,![]() ,
,![]() 即可求解.
即可求解.
![]()
![]()
把![]() 两点代入抛物线
两点代入抛物线![]()
可得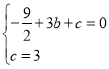
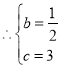
得抛物线解析式为![]()
![]() 点
点![]() 是
是![]() 的平分线与抛物线的交点,
的平分线与抛物线的交点,
![]() 设
设![]() ,代入抛物线
,代入抛物线![]()
得![]() (舍去,因为点
(舍去,因为点![]() 第一象限)
第一象限)
![]()
(2)
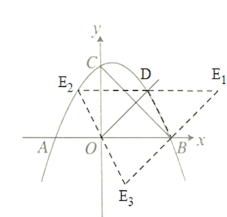
连接BD
若是以OB、OD为邻边的平行四边形
则![]()
故只需把点D向右平移3个单位即得到点![]()
由(1)知D(2,2)
∴![]()
若是以OB、BD为邻边的平行四边形
则![]()
故只需把点D向左平移3个单位即得到点![]()
∴![]()
若是以DB、OD为邻边的平行四边形
则OD∥![]()
则只需把点D向下平移2个单位再向右平移1个单位即得到B,对应地只需把点O向下平移2个单位再向右平移1个单位即得到![]()
∴![]()
综上所述,满足条件的E点坐标为:![]() .
.
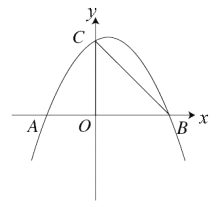
![]() 作直线
作直线![]() 轴于点
轴于点![]() 交
交![]() 于点
于点![]()
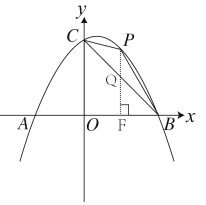
![]() 点坐标为
点坐标为![]()
设直线![]() 的解析式
的解析式![]() .
.
![]()
![]()
解得:![]()
可得直线![]() 解析式为
解析式为![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目