题目内容
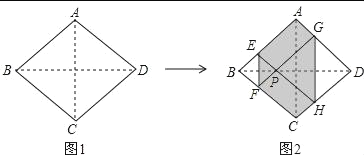
【题目】如图1,正方形纸片ABCD边长为2,折叠∠B和∠D,使两个直角的顶点重合于对角线BD上的一点P,EF、GH分别是折痕(图2),设AE=x(0<x<2),给出下列判断:①x=![]() 时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
时,EF+AB>AC;②六边形AEFCHG周长的值为定值;③六边形AEFCHG面积为定值,其中正确的是( )
A.①②B.①③C.②D.②③
【答案】C
【解析】
由折叠的性质和正方形的性质可得四边形BEPF,四边形PGDH是正方形,四边形AEPG,四边形PFCH是矩形,可得AE=PG=GD=DH=PH=FC,BE=BF=EP=PF=AG=CH,即可判断①②③.
∵折叠,
∴BE=EP,BF=PF,∠ABC=∠EPF=90°,
∵BD平分∠ABC,EF垂直平分BP,
∴BE=BF,
∴四边形BEPF是菱形,且∠EBF=90°,
∴四边形BEPF是正方形,
同理四边形PGDH是正方形,
∴∠AGP=90°,∠AEP=90°,
∴四边形AEPG是矩形,
同理四边形CFPH是矩形,
∴AE=PG=GD=DH=PH=FC,BE=BF=EP=PF=AG=CH,
当x=![]() ,则BE=
,则BE=![]() ,
,
∴EF=![]() ,
,
∴AB+EF=2+![]() ,
,
∵AB=BC=2,
∴AC=2![]()
∴AB+EF<AC,
故①错误;
∵六边形AEFCHG周长=AE+AG+CH+CF+EF+GH=AE+BE+CF+BF+![]() BE+
BE+![]() AE,
AE,
∴六边形AEFCHG周长=AB+BC+![]() (AE+BE)=4+2
(AE+BE)=4+2![]() 是定值,
是定值,
故②正确;
∵六边形AEFCHG面积=2×2﹣![]() BE2﹣
BE2﹣![]() GD2=4﹣
GD2=4﹣![]() (EP2+AE2)=4﹣
(EP2+AE2)=4﹣![]() EG2
EG2
∴六边形AEFCHG面积不是定值,
故③错误.
故选:C.

【题目】某商店销售一种商品,经市场调查发现:该商品的周销售量y(件)是售价x(元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:
售价x(元/件) | 30 | 40 | 60 |
周销售量y(件) | 90 | 70 | 30 |
周销售利润w(元) | 450 | 1050 | 1050 |
注:周销售利润=周销售量×(售价﹣进价)
(1)求y关于x的函数解析式(不要求写出自变量的取值范围);
(2)当售价定为多少时,周销售利润最大,最大利润是多少?
(3)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过45元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1080元,求m的值.