Question

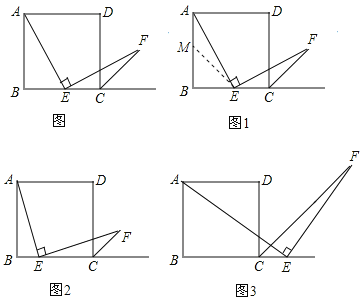
【题目】如图，在等腰Rt△ABC中，∠C=90°，AC=4，矩形DEFG的顶点D、G分别在AC、BC上，边EF在AB上．

（1）求证：△AED∽△DCG；

（2）若矩形DEFG的面积为4，求AE的长．

Answer 1

【答案】（1）见解析；（2） .

【解析】

（1）利用等腰三角形的性质及正方形的性质可求得∠A=∠CDG，∠DEA=∠C，则可证得△AED∽△DCG；

（2）设AE=x，利用矩形的性质及等腰三角形的性质可求得BF=FG=DE=AE=x，从而可表示出EF，结合矩形的面积可得到关于x的方程，则可求得x的值，即可求得AE的长．

（1）证明：∵△ABC是等腰直角三角形，∠C=90°，

∴∠B=∠A=45°，

∵四边形DEFG是矩形，

∴∠AED=∠DEF=90°，DG∥AB，

∴∠CDG=∠A，

∵∠C=90°，

∴∠AED=∠C，

∴△AED∽△DCG；

（2）设AE的长为x，

∵等腰Rt△ABC中，∠C=90°，AC=4，

∴∠A=∠B=45°，AB=4，

∵矩形DEFG的面积为4，

∴DEFE=4，∠AED=∠DEF=∠BFG=90°，

∴BF=FG=DE=AE=x，

∴EF=4-2x，

即x（4-2x）=4，

解得x1=x2=．

∴AE的长为．