题目内容
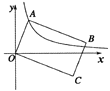
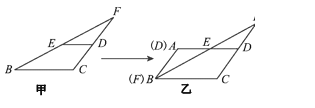
【题目】如图甲,已知ED是△FBC的中位线,沿线段ED将△FED剪下后拼接在图乙中△BEA的位置.
(1)从△FED到△BEA的图形变换,可以认为是(填平移或轴对称或旋转)变换;
(2)试判断图乙中四边形ABCD的形状,并证明你的结论.
【答案】(1)旋转变换;(2)四边形ABCD是平行四边形,见解析
【解析】
(1)由拼接后发现对应点分别是为B与F,A与D,E与E,所以可以得到答案.
(2)利用旋转的性质得到ED=EA,结合中位线的性质得到AD∥BC,AD=BC可以得出结论.
解:(1)拼接后,B与F是对应点,A与D是对应点,E与自身对应,所以是旋转对称关系,即旋转变换.
(2)四边形ABCD是平行四边形
证明:∵△FED到△BEA是旋转变换,
∴ED=EA.∴AD=2ED.
∵ED是△FBC的中位线,
∴ED∥CB,CB=2DE,
∴AD∥BC,AD=BC.
∴四边形ABCD是平行四边形.

练习册系列答案
相关题目