题目内容
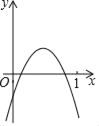
【题目】已知二次函数
图象的顶点横坐标是2，与x轴交于A（x1，0）、
B（x2，0），x1﹤0﹤x2，与y轴交于点C，O为坐标原点，
．
（1）求证：
；
（2）求m、n的值；
（3）当p﹥0且二次函数图象与直线
仅有一个交点时，求二次函数的最大值．
【答案】（1）证明：∵二次函数
图象的顶点横坐标是2，
∴抛物线的对称轴为x=2，即
，化简得：n+4m=0．
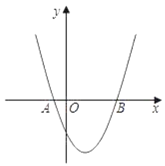
（2）解：∵二次函数与x轴交于A（x1，0）、B（x2，0），x1＜0＜x2，
∴OA=－x1，OB=x2；
．
令x=0，得y=p，∴C（0，p），∴OC=|p|．
由三角函数定义得：
．
∵tan∠CAO－tan∠CBO=1，即
，化简得：
．
将代入得：
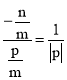，化简得：
．
由（1）知n+4m=0，
∴当n=1时，
；当n=－1时，
．
∴m、n的值为：，n=－1（此时抛物线开口向上）或，n=1（此时抛物线开口向下）．
（3）解：由（2）知，当p＞0时，n=1，，
∴抛物线解析式为：
．
联立抛物线与直线y=x+3解析式得到：
，
化简得：
．
∵二次函数图象与直线y=x+3仅有一个交点，
∴一元二次方程＊根的判别式等于0，即△=02+16（p－3）=0，解得p=3．
∴抛物线解析式为：
．
当x=2时，二次函数有最大值，最大值为4．
∴当p＞0且二次函数图象与直线y=x+3仅有一个交点时，二次函数的最大值为4．
【解析】
二次函数综合题，曲线上点的坐标与方程的关系，一元二次方程根的判别式和根与系数的关系，锐角三角函数定义，二次函数的性质．
（1）由题意可知抛物线的对称轴为x=2，利用对称轴公式，化简即得n+4m=0．
（2）利用三角函数定义和抛物线与x轴交点坐标性质求解．特别需要注意的是抛物线的开口方向未定，所以所求m、n的值将有两组．
（3）利用一元二次方程的判别式等于0求解．当p＞0时，m、n的值随之确定；将抛物线的解析式与直线的解析式联立，得到一个一元二次方程；由交点唯一可知，此一元二次方程的判别式等于0，据此求出p的值，从而确定了抛物线的解析式；最后由抛物线的解析式确定其最大值．
