Question

【题目】已知关于x的不等式组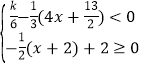有且只有四个整数解，又关于x的分式方程﹣2=有正数解，则满足条件的整数k的和为（　　）

A. 5 B. 6 C. 7 D. 8

Answer 1

【答案】D

【解析】

根据不等式组求出k的范围，然后再根据分式方程求出k的范围，从而确定的k的可能值．

解不等式-(4x+)＜0，

得：x＞，

解不等式﹣(x+2)+2≥0，得：x≤2，

则不等式组的解集为＜x≤2，

∵不等式组有且只有四个整数解，

∴﹣2≤＜﹣1，

解得:﹣3≤k＜5；

解分式方程-2= 得：x=，

∵分式方程有正数解，

∴＞0，且 ≠1，

解得：k＞﹣3且k≠﹣1，

所以满足条件的整数k的值为﹣2、0、1、2、3、4，

则满足条件的整数k的和为﹣2+0+1+2+3+4=8，

故选：D.