题目内容
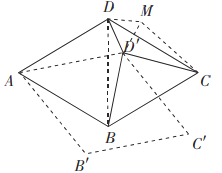
【题目】综合与实践:问题情境:在一次综合实践活动课上,同学们以菱形为对象,研究菱形旋转中的问题:已知,在菱形![]() 中,
中,![]() 为对角线,
为对角线,![]() ,
,![]() ,将菱形
,将菱形![]() 绕顶点
绕顶点![]() 顺时针旋转,旋转角为
顺时针旋转,旋转角为![]() (单位
(单位![]() ).旋转后的菱形为
).旋转后的菱形为![]() .在旋转探究活动中提出下列问题,请你帮他们解决.
.在旋转探究活动中提出下列问题,请你帮他们解决.
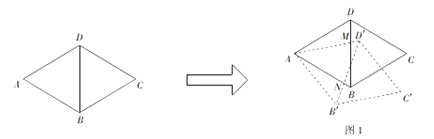
(1)如图1,若旋转角![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() .请说明线段
.请说明线段![]() 与
与![]() 的数量关系;
的数量关系;
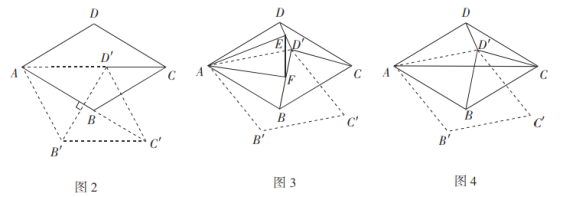
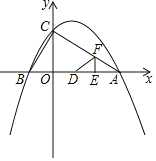
(2)如图2,连接![]() ,菱形
,菱形![]() 旋转的过程中,当
旋转的过程中,当![]() 与
与![]() 互相垂直时,
互相垂直时,![]() 的长为______;
的长为______;
(3)如图3,若旋转角为![]() 时,分别连接
时,分别连接![]() ,
,![]() ,过点
,过点![]() 分别作
分别作![]() ,
,![]() ,连接
,连接![]() ,菱形
,菱形![]() 旋转的过程中,发现在
旋转的过程中,发现在![]() 中存在长度不变的线段
中存在长度不变的线段![]() ,请求出
,请求出![]() 长度;
长度;
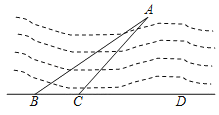
操作探究:(4)如图4,在(3)的条件下,请判断以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是什么特殊三角形,并说明理由.
三条线段长度为边的三角形是什么特殊三角形,并说明理由.
【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ;(3)EF=2;(4)
;(3)EF=2;(4)![]() ,
,![]() ,
,![]() 三条线段为边的三角形是直角三角形,理由见解析
三条线段为边的三角形是直角三角形,理由见解析
【解析】
(1)根据菱形的性质以及旋转的性质,证得![]() ,根据
,根据![]() 证得
证得![]() ,可以得到结论;
,可以得到结论;
(2)根据菱形的性质及 条件![]() 与
与![]() 互相垂直,证明A、D、C在同一直线上,利用锐角三角函数求得对角线的长,即可求得结论;
互相垂直,证明A、D、C在同一直线上,利用锐角三角函数求得对角线的长,即可求得结论;
(3)利用等腰三角形三线合一的性质,EF是![]() 的中位线,从而证明
的中位线,从而证明![]() =2;
=2;
(4)以![]() 为边向外作等边三角形,利用等边三角形的性质以及SAS证明
为边向外作等边三角形,利用等边三角形的性质以及SAS证明![]() ,得到
,得到![]() ,把
,把![]() 、
、![]() 、
、![]() 三条线段归结到一个三角形中,易证得
三条线段归结到一个三角形中,易证得![]() 是直角三角形,从而得到结论.
是直角三角形,从而得到结论.
(1)![]() ,理由如下:
,理由如下:
∵四边形![]() 是菱形,∴
是菱形,∴![]() .
.
∴![]() .
.
由旋转的性质可得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
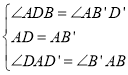 ,
,
∴![]() ,∴
,∴![]() .
.
(2)菱形AB'CD'中,B'D'=AB ,∠B'AD'=60° ,
AB平分∠B'AD' (等腰三角形三线合一),
∴∠BAD'=30°,
∵∠B_AD= 60°,
∴∠BAD'=∠D'AD=30°,
∴A 、D、C在同一直线上,
如图,菱形ABCD中, BD为对角线,∠BAD= 60°,AB=4,
∴∠DAG=∠BAG=30°,AC=2AG
∴![]() ,
,![]()
∴![]() ,
,
∴![]()
![]() ,
,
故答案为: ![]()
(3)如图,连接![]() ,由题可得:
,由题可得:![]() .
.
∵![]() ,
,
∴![]() (等腰三角形三线合一),同理
(等腰三角形三线合一),同理![]() ,
,
∴![]() 是
是![]() 的中位线,∴
的中位线,∴![]() .
.
∵四边形![]() 是菱形,∴
是菱形,∴![]() ,
,
又∵![]() ,
,![]() 是等边三角形,
是等边三角形,
∴![]() ,∴
,∴![]() .
.
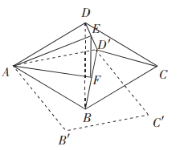
(4)以![]() ,
,![]() ,
,![]() 三条线段为边的三角形是直角三角形,理由如下:
三条线段为边的三角形是直角三角形,理由如下:
如图,以![]() 为边向外作等边三角形
为边向外作等边三角形![]() ,连接
,连接![]() ,
,![]() ,
,
∵四边形![]() 是菱形,
是菱形,![]() ,
,
∴![]() 与
与![]() 是等边三角形,
是等边三角形,![]() .
.
由(3)可知:![]() 与
与![]() 都是等腰三角形,
都是等腰三角形,
∴![]()
![]()
![]()
![]() .
.
∵![]() 与
与![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() .
.
在![]() 和
和![]() 中,
中,
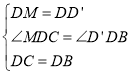 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
![]() .
.
∴![]() 是直角三角形,
是直角三角形,
即以![]() ,
,![]() ,
,![]() 三条线段长度为边的三角形是直角三角形.
三条线段长度为边的三角形是直角三角形.

【题目】我们约定:体重在选定标准的![]() %(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
%(包含)范围之内时都称为“一般体重”.为了解某校七年级男生中具有“一般体重”的人数,我们从该校七年级男生中随机选出10名男生,测量出他们的体重(单位:kg),收集并整理得到如下统计表:
男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
体重 | 45 | 62 | 55 | 58 | 67 | 80 | 53 | 65 | 60 | 55 |
根据以上表格信息解决如下问题:
(1)将这组数据的三个统计量:平均数、中位数和众数填入下表:
平均数 | 中位数 | 众数 |
(2)请你选择其中一个统计量作为选定标准,说明选择的理由.并按此选定标准找出这10名男生中具有“一般体重”的男生.