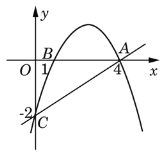
题目内容
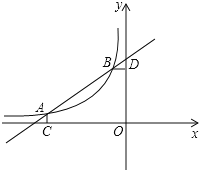
【题目】如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
(1)求出抛物线的解析式;
(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1) y=-![]() x2+
x2+![]() x-2;(2)点P为(2,1)或(5,-2)或(-3,-14)或(0,-2).
x-2;(2)点P为(2,1)或(5,-2)或(-3,-14)或(0,-2).
【解析】
(1)用待定系数法求出抛物线解析式;
(2)以A、P、M为顶点的三角形与△OAC相似,分两种情况讨论计算即可.
解:(1)∵该抛物线过点C(0,-2),
∴可设该抛物线的解析式为y=ax2+bx-2.
将A(4,0),B(1,0)代入,得![]() ,解得
,解得 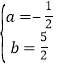 ,
,
∴此抛物线的解析式为![]() .
.
(2)存在,
设P点的横坐标为m,则P点的纵坐标为-![]() m2+
m2+![]() m-2,
m-2,
当1<m<4时,AM=4-m,PM=-![]() m2+
m2+![]() m-2.又∵∠COA=∠PMA=90°,
m-2.又∵∠COA=∠PMA=90°,
∴①当![]() =
=![]() =
=![]() 时,△APM∽△ACO,即4-m=2(-
时,△APM∽△ACO,即4-m=2(-![]() m2+
m2+![]() m-2).
m-2).
解得m1=2,m2=4(舍去),∴P(2,1).
②当![]() =
=![]() =
=![]() 时,△APM∽△CAO,即2(4-m)=-
时,△APM∽△CAO,即2(4-m)=-![]() m2+
m2+![]() m-2.
m-2.
解得m1=4,m2=5(均不合题意,舍去),∴当1<m<4时,P(2,1).
类似地可求出当m>4时,P(5,-2).
当m<1时,P(-3,-14)或P(0,-2),
综上所述,符合条件的点P为(2,1)或(5,-2)或(-3,-14)或(0,-2).

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目