题目内容
如图,直角梯形ABCD中,AB∥CD,∠C=90°,∠BDA=90°,AB=a,BD=b,CD=c,BC=d,AD=e,则下列等式成立的是
| A.b2=ac | B.b2=ce | C.be=ac | D.bd=ae |
A
解析试题分析:∵CD∥AB,∴∠CDB=∠DBA。
又∵∠C=∠BDA=90°,∴△CDB∽△DBA。∴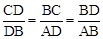 ,即
,即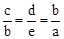 。
。
∴A、b2=ac,成立,故本选项正确;
B、b2=ac,不是b2=ce,故本选项错误;
C、be=ad,不是be=ac,故本选项错误;
D、bd=ac,不是bd=ae,故本选项错误。
故选A。

练习册系列答案
相关题目
如图,在Rt△ABC中,∠C=90°,P是斜边上一定点,过点P作直线与一直角边交于点Q使图中出现两个相似三角形,这样的点Q有 ( )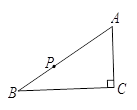
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,在△ABC中,若∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为( )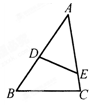
A. | B.7 | C.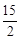 | D. |
 (顶点均在格点上),若它们是以点P为位似中心的位似图形,则点P的坐标是( )
(顶点均在格点上),若它们是以点P为位似中心的位似图形,则点P的坐标是( )

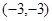







 ABCD中,AB=6、AD=9,∠BAD的平分线交BC于点E,DC的延长线于点F, BG⊥AE,垂足为G,若BG=4
ABCD中,AB=6、AD=9,∠BAD的平分线交BC于点E,DC的延长线于点F, BG⊥AE,垂足为G,若BG=4 ,则△CEF的面积是
,则△CEF的面积是

 B.
B. C.
C. D.
D.
 分别是
分别是 的边
的边 上的点,
上的点, ,
, ,则
,则 ;
;