ƒøƒ⁄»›
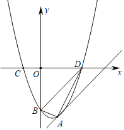
°æƒø°ø»ÁÕº£¨≈◊ŒÔœfly£Ωax2+bx©Å4a£®a°Ÿ0£©æ≠π˝A£®©Å1£¨0£©°¢C£®0£¨4£©¡Ωµ„£¨”Îx÷·Ωª”⁄¡Ì“ªµ„B£¨¡¨Ω”AC£¨BC£Æ
£®1£©«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£ª
£®2£©π˝µ„C◊˜x÷·µƒ∆Ω––œflΩª≈◊ŒÔœfl”⁄¡Ì“ªµ„D£¨¡¨Ω”BD£¨µ„PŒ™≈◊ŒÔœfl…œ“ªµ„£¨«“°œDBP£Ω45°„£¨«Ûµ„Pµƒ◊¯±Í£ª
£®3£©‘⁄≈◊ŒÔœflµƒ∂‘≥∆÷·…œ «∑ҥʑ⁄µ„M£¨ πµ√”…µ„M£¨A£¨Cππ≥…µƒ°˜MAC «÷±Ω«»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„Mµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©y£Ω©Åx2+3x+4£ª£®2£©P£®©Å![]() £¨
£¨![]() £©£ª£®3£©µ„Mµƒ◊¯±ÍŒ™£®
£©£ª£®3£©µ„Mµƒ◊¯±ÍŒ™£®![]() £¨
£¨![]() £©ªÚ£®
£©ªÚ£®![]() £¨©Å
£¨©Å![]() £©ªÚ£®
£©ªÚ£®![]() £¨
£¨![]() £©ªÚ£®
£©ªÚ£®![]() £¨
£¨![]() £©£Æ
£©£Æ
°æΩ‚Œˆ°ø
£®1£©-4a=4£¨Ω‚µ√£∫a=-1£¨‘Ú≈◊ŒÔœflµƒ±Ì¥Ô ΩŒ™£∫y=-x2+bx+4£¨Ω´µ„Aµƒ◊¯±Í¥˙»Î…œ Ω≤¢Ω‚µ√£∫b=3£¨º¥ø…«ÛΩ‚£ª
£®2£©…Ë£∫HR=BR=x£¨‘ÚER=4x£¨BD=5x=![]() £Ω
£Ω![]() £¨x£Ω
£¨x£Ω![]() £¨BH£Ω
£¨BH£Ω![]() x£¨BG£Ω1£¨‘ÚGH£Ω
x£¨BG£Ω1£¨‘ÚGH£Ω![]() £Ω
£Ω![]() £¨π µ„H£®3£¨
£¨π µ„H£®3£¨![]() £©£¨∂¯µ„B£®4£¨0£©£¨÷±œflHBµƒ±Ì¥Ô ΩŒ™£∫y=
£©£¨∂¯µ„B£®4£¨0£©£¨÷±œflHBµƒ±Ì¥Ô ΩŒ™£∫y= ![]() °≠¢⁄£¨
°≠¢⁄£¨
¡™¡¢¢Ÿ¢⁄≤¢Ω‚µ√£∫x=4ªÚ-![]() £®…·»•4£©£¨º¥ø…«ÛΩ‚£ª
£®…·»•4£©£¨º¥ø…«ÛΩ‚£ª
£®3£©∑÷AM «–±±fl°¢CM «–±±fl°¢AC «–±±fl»˝÷÷«Èøˆ£¨∑÷±«ÛΩ‚º¥ø…£Æ
£®1£©©Å4a£Ω4£¨Ω‚µ√£∫a£Ω©Å1£¨
‘Ú≈◊ŒÔœflµƒ±Ì¥Ô ΩŒ™£∫y£Ω©Åx2+bx+4£¨
Ω´µ„Aµƒ◊¯±Í¥˙»Î…œ Ω≤¢Ω‚µ√£∫b£Ω3£¨
π ≈◊ŒÔœflµƒ±Ì¥Ô ΩŒ™£∫y£Ω©Åx2+3x+4°≠¢Ÿ£ª
£®2£©≈◊ŒÔœflµƒ∂‘≥∆÷·Œ™£∫x£Ω![]() £¨µ„D£®3£¨4£©£¨
£¨µ„D£®3£¨4£©£¨
π˝µ„D◊˜x÷·µƒ¥πœflΩªBP”⁄µ„H£¨Ωªx÷·”⁄µ„G£¨
π˝µ„H◊˜HR°ÕBD”ε„R£¨
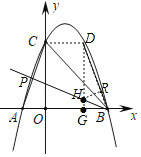
‘ÚBG£Ω1£¨GD£Ω4£¨tan°œBDG£Ω![]() £¨°œDBP£Ω45°„£¨
£¨°œDBP£Ω45°„£¨
…Ë£∫HR£ΩBR£Ωx£¨‘ÚDR£Ω4x£¨ BD£Ω5x£Ω![]() £Ω
£Ω![]() £¨x£Ω
£¨x£Ω![]() £¨ BH£Ω
£¨ BH£Ω![]() x£¨BG£Ω1£¨‘ÚGH£Ω
x£¨BG£Ω1£¨‘ÚGH£Ω![]() £Ω
£Ω![]() £¨π µ„H£®3£¨
£¨π µ„H£®3£¨![]() £©£¨∂¯µ„B£®4£¨0£©£¨Õ¨¿Ìø…µ√÷±œflHBµƒ±Ì¥Ô ΩŒ™£∫y£Ω©Å
£©£¨∂¯µ„B£®4£¨0£©£¨Õ¨¿Ìø…µ√÷±œflHBµƒ±Ì¥Ô ΩŒ™£∫y£Ω©Å![]() x+
x+![]() °≠¢⁄£¨
°≠¢⁄£¨
¡™¡¢¢Ÿ¢⁄≤¢Ω‚µ√£∫x£Ω4ªÚ©Å![]() £®…·»•4£©£¨
£®…·»•4£©£¨
𠵄P£®©Å![]() £¨
£¨![]() £©£ª
£©£ª
£®3£©…˵„M£®![]() £¨m£©£¨∂¯µ„A£®©Å1£¨0£©°¢µ„C£®0£¨4£©£¨‘ÚAM2£Ω
£¨m£©£¨∂¯µ„A£®©Å1£¨0£©°¢µ„C£®0£¨4£©£¨‘ÚAM2£Ω![]() +m2£¨CM2£Ω
+m2£¨CM2£Ω![]() +£®m©Å4£©2£¨AC2£Ω17£¨
+£®m©Å4£©2£¨AC2£Ω17£¨
¢Ÿµ±AM «–±±fl ±£¨![]() +m2£Ω
+m2£Ω![]() +£®m©Å4£©2+17£¨Ω‚µ√£∫m£Ω
+£®m©Å4£©2+17£¨Ω‚µ√£∫m£Ω![]() £ª
£ª
¢⁄µ±CM «–±±fl ±£¨Õ¨¿Ìø…µ√£∫m£Ω©Å![]() £ª
£ª
¢€µ±AC «–±±fl ±£¨Õ¨¿Ìø…µ√£∫m£Ω![]() ªÚ
ªÚ![]() £ª
£ª
◊€…œ£¨µ„Mµƒ◊¯±ÍŒ™£∫£®![]() £¨
£¨![]() £©ªÚ£®
£©ªÚ£®![]() £¨©Å
£¨©Å![]() £©ªÚ£®
£©ªÚ£®![]() £¨
£¨![]() £©ªÚ£®
£©ªÚ£®![]() £¨
£¨![]() £©£Æ
£©£Æ

 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏