题目内容
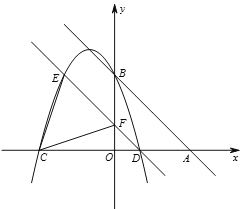
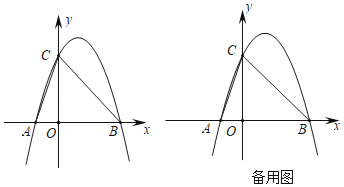
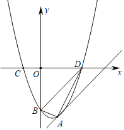
【题目】如图,抛物线y=x2﹣2x+c的顶点A在直线l:y=x﹣a上,点D(3,0)为抛物线上一点.
(1)求a的值;
(2)抛物线与y轴交于点B,试判断△ABD的形状.
【答案】(1)5;(2)直角三角形.
【解析】
(1)根据点D的坐标可求出抛物线的解析式,进而求出顶点A的坐标,将A代入直线方程可求出![]() 的值.
的值.
(2)令抛物线中的![]() 求出点B的坐标,然后求出
求出点B的坐标,然后求出![]() 三边的长,进而判断三角形的形状即可.
三边的长,进而判断三角形的形状即可.
解:(1)∵点D(3,0)在抛物线y=x2﹣2x+c
∴9﹣6+c=0,
∴c=﹣3.
由y=x2﹣2x﹣3=(x﹣1)2﹣4,得顶点A为(1,﹣4)
∵顶点A在直线y=x﹣a上,
∴当x=1时,
∴y=1﹣a=﹣4,
∴a=5;
(2)△ABD是直角三角形;
由(1)可知,y=x2﹣2x﹣3,
∴B(0,﹣3),
BD2=OB2+OD2=18,AB=(4﹣3)2+12=2,AD=(3﹣1)2+42=20,
BD2+AB2=AD2,
∴∠ABD=90°,即△ABD是直角三角形.

练习册系列答案
相关题目
【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.