题目内容
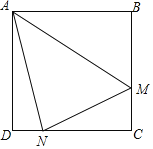
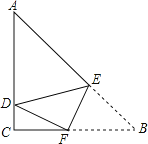
【题目】如图,菱形![]() 和菱形
和菱形![]() 的边长分别为4和6,
的边长分别为4和6,![]() ,则阴影部分的面积是( )
,则阴影部分的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
设BF交CE于点H,根据菱形的对边平行,利用相似三角形对应边成比例列式求出CH,然后求出DH,根据菱形邻角互补求出∠ABC=60°,再求出点B到CD的距离以及点G到CE的距离;然后根据阴影部分的面积=S△BDH+S△FDH,根据三角形的面积公式列式进行计算即可得解.
如图,设BF交CE于点H,过B点作BM⊥DC交DC的延长线于M点,过F点作FN⊥CD交CD的延长线于N点.
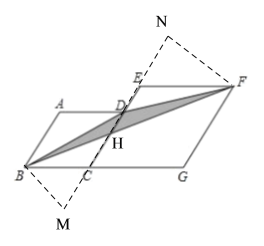
∵菱形ECGF的边CE∥GF,
∴△BCH∽△BGF,
∴![]() ,
,
即![]()
解得CH=![]()
所以,DH=CD-CH=4-![]() =
=![]() ,
,
∵四边形![]() 和四边形
和四边形![]() 是菱形,∠A=120°,
是菱形,∠A=120°,
∴AD∥BC,AB∥CD,EF∥CG
∴∠NEF=∠ECG=∠BCM=∠ABC=180°-120°=60°,
∴BM=BC×sin60°=4×![]() =2
=2![]()
FN=EF×sin60°=6×![]() =3
=3![]()
∴阴影部分的面积=S△BDH+S△FDH,
=![]()
故选:C

练习册系列答案
相关题目
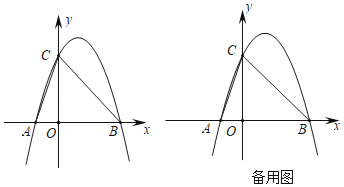
【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.