题目内容
【题目】如图,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() .
.
(1)求![]() 的长;
的长;
(2)点![]() 为直线
为直线![]() 上的一个动点,连接
上的一个动点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 的角度后得到对应的线段
的角度后得到对应的线段![]() (即
(即![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
①当![]() 时,求
时,求![]() 的长;
的长;
②连接![]() 、
、![]() ,当
,当![]() 的长度最小时,求
的长度最小时,求![]() 的面积.
的面积.

【答案】(1)8;(2)①![]() ;②当DF的长度最小时,△ACF的面积为
;②当DF的长度最小时,△ACF的面积为![]() .
.
【解析】
(1)利用菱形的性质,把所求的BD的一半BO放到Rt△AOB中用勾股定理求解即可;
(2)①当![]() 时,可利用△ACD的面积求出CE的长度,因为已知条件中有相等的角∠ECF=∠BCD,所以寻找△CEF是否与△BCD相似,然后利用相似三角形对应边成比例即可求出EF的长度;
时,可利用△ACD的面积求出CE的长度,因为已知条件中有相等的角∠ECF=∠BCD,所以寻找△CEF是否与△BCD相似,然后利用相似三角形对应边成比例即可求出EF的长度;
②如果直接求△ACF面积的最小值并不好求,因为只有一边AC已知,而AC边上的高的最小值并不好确定,所以想办法进行转化.通过题目中的已知条件发现△BCE≌△DCF,从而得出BE=DF,所以当DF最小时,也就是BE最小时.当BE⊥DE时,BE最小,从而可利用相似求出△ACF面积的最小值.
解:(1)∵四边形ABCD是菱形,
∴AD=AB=BC=CD=![]() ,AC⊥BD,
,AC⊥BD,
OA=OC=![]() AC=
AC=![]() ,OB=OD,
,OB=OD,
在Rt△AOB中,由勾股定理得:![]()
∴BD=2OB=8;
(2)①![]()
∴![]()
∴![]()
由旋转的性质得:∠ECF=∠BCD,CF=CE,
∴![]()
![]() ,
,
∴△ECF∽△BCD,
∴![]() ,
,
∴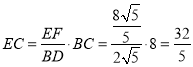 ;
;
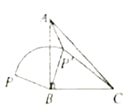
②如图所示:
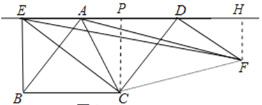
∵∠BCD=∠ECF
∴∠BCD-∠ECD =∠ECF-∠ECD
∴∠BCE=∠DCF
在△BCE和△DCF中,
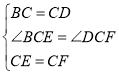
∴△BCE≌△DCF(SAS),
∴BE=DF,![]()
当BE最小时,DF就最小,且BE⊥DE
此时∠EBC=∠FDC=90°,BE=DF=4
∵△BCE,△ABC,△ACD等底等高
∴![]()
∴![]()
∴![]()
过点F作FH⊥AD于H,过点C作CP⊥AD于P,
则∠CPD=90°,
∴∠PCD+∠PDC=90°,
∵∠FDC=90°,
∴∠PDC+∠HDF=90°,
∴∠PCD=∠HDF,
∴△PCD∽△HDF,
∴![]() ,
,
∴HF=![]() ,
,
∴S△ADF=![]() ADHF=
ADHF=![]() ,
,
∴S△ACF=S四边形ACFD﹣S△ADF=16﹣![]() =
=![]() ,
,
即当DF的长度最小时,△ACF的面积为![]() .
.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案