题目内容
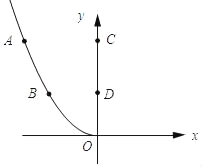
【题目】中国高铁迅猛发展，给我们的出行带来极大的便捷，如图1，是某种新设计动车车头的纵截面一部分，曲线OBA是一开口向左，对称轴正好是水平线OC的抛物线的一部分，点A、B是车头玻璃罩的最高点和最低点，AC、BD是两点到车厢底部的距离，OD=1.5米，BD=1.5米，AC=3米，请你利用所学的函数知识解决以下问题．
（1）为了方便研究问题，需要把曲线OBA绕点O旋转转化为我们熟悉的函数，请你在所给的方框内，画出你旋转后函数图象的草图，在图中标出点O、A、B、C、D对应的位置，并求你所画的函数的解析式．
（2）如图2，驾驶员座椅安装在水平线OC上一点P处，实验表明：当PA+PB最小时，驾驶员驾驶时视野最佳，为了达到最佳视野，求OP的长．
（3）驾驶员头顶到玻璃罩的高度至少为0.3米才感到压抑，一个驾驶员坐下时头顶到椅面的距离为1米，在（2）的情况下，座椅最多条件到多少时他才感到舒适？
【答案】（1）函数的解析式为y=
x2（x≤0）；（2）OP= 3．（3）座椅最多调节得到0.8米时，他才感到舒适．
【解析】试题分析：（1）由图像的特点知，将曲线OBA绕点O逆时针旋转90°后变为我们熟悉的二次函数，旋转后点B的坐标为（﹣1.5，1.5），然后用待定系数法求出解析式；
（2）作点A关于OC的对称点A′，连结BA′交OC与点P．设DP=x，则PC=4.5﹣x，由
△CA′P∽△DBP列方程求解；
（3）将y=3代入（1）中所求的函数关系式，求出x的值，从而可求出答案.
解：（1）将曲线OBA绕点O逆时针旋转90°如图所示：则B（﹣1.5，1.5）．
设所画函数的解析式为y=ax2，将点B的坐标代入得：
a=
，解得：a=
．
∴函数的解析式为y=
x2．（x≤0）
（2）如下图所示：作点A关于OC的对称点A′，连结BA′交OC与点P．
由（1）可知OC=×32=6，则DC=OC﹣OD=4.5．
∵BD∥CA，
∴△CA′P∽△DBP．
∴
=
．
设DP=x，则PC=4.5﹣x．
∴
=
，解得：x=1.5．
∴DP=1.5．
∴OP=OD+DP=3．
（3）将y=3代入y=x2（x≤0），得： x2=3，解得：x=﹣
或x=（舍去）．
∴点P到玻璃罩的高度=
≈2.1．
∵2.1﹣0.3﹣1=0.8．
∴座椅最多调节得到0.8米时，他才感到舒适．
【题目】我市某中学举行“中国梦校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛．两个队各选出的5名选手的决赛成绩如图4所示．
（1）根据图示填写下表：
平均数（分） | 中位数（分） | 众数（分） | |
初中部 | 85 | ||
高中部 | 85 | 100 |
（2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
（3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定．
【题目】将一张正方形纸片剪成四个大小、形状一样的小正方形（如图所示），记为第一次操作，然后将其中的一片又按同样的方法剪成四小片，记为第二次操作，如此循环进行下去．请将下表中空缺的数据填写完整，并解答所提出的问题：
操作次数 | 1 | 2 | 3 | 4 | … |
正方形个数 | 4 | 7 |
|
| … |
（1）如果剪100次，共能得到 个正方形；
（2）如果剪n次共能得到bn个正方形，试用含有n、bn的等式表示它们之间的数量关系 ；
（3）若原正方形的边长为1，设an表示第n次所剪的正方形的边长，试用含n的式子表示an ；
（4）试猜想a1+a2+a3+a4+…+an﹣1+an与原正方形边长的数量关系，并用等式写出这个关系 ．
