题目内容
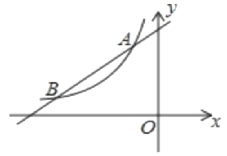
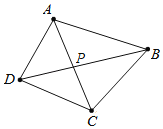
【题目】如图,已知四点A、B、C、D;
(1)画射线AD;(不需写作图过程)
(2)求作点P,使PA+PB+PC+PD的值最小;(不需写作图过程)
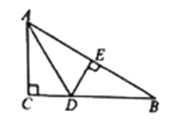
(3)在(2)的条件下,若S△ABP=2,S△ADP=6,S△BCP=1.5,则S△DCP= .
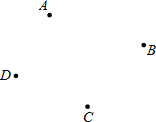
【答案】(1)见解析;(2)见解析;(3)4.5.
【解析】
(1)根据射线的定义作图;
(2)使PA+PB+PC+PD的值最小的点P,应在AC、BD连线的交点上,由此画出即可;
(3)根据同高三角形面积的比等于对应底边的比,所以![]() =
=![]() ,可计算结论.
,可计算结论.
解:(1)如图:
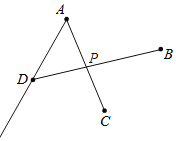
(2)连接AC、BD交于点P;
(3)如图,∵S△ABP=2,S△ADP=6,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵S△BCP=1.5,
∴S△DCP=4.5,故答案为:4.5.

【题目】我市某中学举行“中国梦校园好声音”歌手大赛,初、高中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图4所示.

(1)根据图示填写下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
【题目】将一张正方形纸片剪成四个大小、形状一样的小正方形(如图所示),记为第一次操作,然后将其中的一片又按同样的方法剪成四小片,记为第二次操作,如此循环进行下去.请将下表中空缺的数据填写完整,并解答所提出的问题:
操作次数 | 1 | 2 | 3 | 4 | … |
正方形个数 | 4 | 7 |
|
| … |
(1)如果剪100次,共能得到 个正方形;
(2)如果剪n次共能得到bn个正方形,试用含有n、bn的等式表示它们之间的数量关系 ;
(3)若原正方形的边长为1,设an表示第n次所剪的正方形的边长,试用含n的式子表示an ;
(4)试猜想a1+a2+a3+a4+…+an﹣1+an与原正方形边长的数量关系,并用等式写出这个关系 .