题目内容
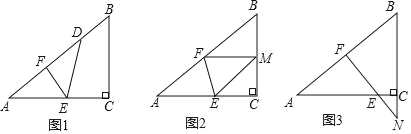
【题目】如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=![]() ,求
,求![]() 的值.
的值.
【答案】(1)2![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)先利用折叠的性质得到![]() ,
, ![]() ≌
≌![]() ,则
,则![]() 则易得S△ABC=5S△AEF,再证明
则易得S△ABC=5S△AEF,再证明![]() 然后根据相似三角形的性质得到
然后根据相似三角形的性质得到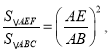 再利用勾股定理求出AB即可得到AE的长;
再利用勾股定理求出AB即可得到AE的长;
(2)①通过证明四条边相等判断四边形AEMF为菱形;
②连结AM交EF于点O,如图②,设![]() 则
则![]() 先证明
先证明![]() 得到
得到![]() 解出
解出![]() 后计算出
后计算出![]() 再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
再利用勾股定理计算出AM,然后根据菱形的面积公式计算EF;
(3)如图③,作作![]() 于H,先证明
于H,先证明![]() 利用相似比得到
利用相似比得到![]() 设
设![]() ,则
,则![]()
![]() 再证明
再证明![]() 利用相似比可计算出
利用相似比可计算出![]() 则可计算出
则可计算出![]() 和
和![]() ,接着利用勾股定理计算出
,接着利用勾股定理计算出![]() ,从而得到
,从而得到![]() 的长,于是可计算出
的长,于是可计算出![]() 的值.
的值.
试题解析:(1)∵![]() 的一角沿EF折叠,折叠后点A落在AB边上的点D处,
的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴![]() ,
, ![]() ≌
≌![]() ,
,
∴![]()
∵S四边形ECBF=![]()
∴S△ABC=5S△AEF,
在Rt ![]() 中,∵
中,∵![]()
∴![]()
∵![]()
∴![]()
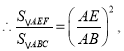
即![]()
∴![]()
由折叠知, ![]()
(2)①连结AM交EF于点O,如图2,

∵![]() 的一角沿EF折叠,折叠后点A落在AB边上的点D处,
的一角沿EF折叠,折叠后点A落在AB边上的点D处,
∴![]()
∵MF∥AC,
∴![]()
∴![]()
∴![]()
∴![]()
∴四边形AEMF为菱形,
②设![]() 则
则![]()
∵四边形AEMF为菱形,
∴EM∥AB,
∴![]()
∴![]()
即![]()
解得![]()
在Rt ![]() 中,
中, ![]()
∵S菱形AEMF![]()
∴![]()
(3)如图③,作![]() 于H,
于H,
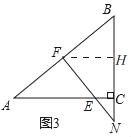
∵EC∥FH,
∴![]()
∴![]()
∴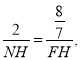
∴![]()
设![]() ,则
,则![]()
![]()
∵FH∥AC,
∴![]()
∴![]()
![]()
∴![]()
∴![]()
在Rt ![]() 中,
中, ![]()
∴![]()
∴![]()

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案