题目内容
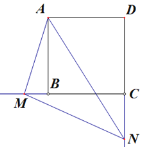
【题目】已知，正方形ABCD，M在CB延长线上，N在DC延长线上，∠MAN=45°．求证：MN=DN-BM．
【答案】详见解析
【解析】
根据题意作辅助线AH⊥MN，垂足为H以及在DN上截取DE=MB，连接AE，证△ABM≌△ADE，推出AM=AE；∠MAB=∠EAD，求出∠EAN=∠MAN，根据SAS证△AMN≌△AEN，推出MN=EN即可.
解：如图，作辅助线AH⊥MN，垂足为H，并在DN上截取DE=MB，连接AE，
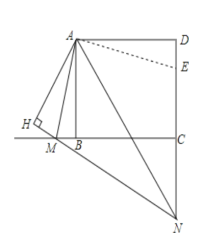
在正方形ABCD中，
∵AD=AB，∠D=∠ABM=90°，
在△ABM与△ADE中，
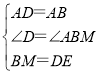
∴△ABM≌△ADE，
∴AM=AE，∠MAB=∠EAD，
∵∠MAN=45°=∠MAB+∠BAN，
∴∠DAE+∠BAN=45°，
∴∠EAN=90°-45°=45°=∠MAN，
在△AMN和△AEN中，
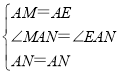
∴△AMN≌△AEN，
∴MN=EN，
∵DN-DE=EN，
∴MN=DN-BM．
练习册系列答案
相关题目
【题目】已知二次函数
的
与
的部分对应值如表：
|
|
|
|
|
|
|
|
|
|
|
|
下列结论：
抛物线的开口向上；②抛物线的对称轴为直线
；③当
时，
；④抛物线与轴的两个交点间的距离是
；⑤若
是抛物线上两点，则
，其中正确的个数是（ ）
A.
B.
C.D.
