题目内容
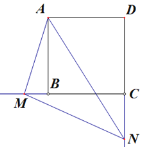
【题目】为倡导“绿色出行,低碳生活”的号召,今年春天,安庆市的街头出现了一道道绿色的风景线--“共享单车”. 图(1)所示的是一辆共享单车的实物图. 图(2)是这辆共享单车的部分几何示意图,其中车架档AC长为40cm,座杆CE的长为18cm. 点A、C、E在同一条直线上,且∠CAB=60°,∠ACB=75°
(1)求车座点E到车架档AB的距离;
(2)求车架档AB的长.

【答案】(1)车座点E到车架档AB的距离为![]() ;(2)车架档AB的长为
;(2)车架档AB的长为![]()
【解析】
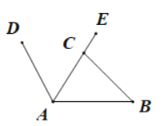
(1)过E作EF⊥AB,垂足为F,运用EF=AE·sin∠CAB=58sin60°可得;
(2)过C作CG⊥AB,垂足为G,可得AG=AC·cos∠CAB=40cos60°,CG=AC·sin∠CAB=40sin60°,在Rt△BCG中,则BG=CG=![]() cm,故AB=AG+BG.
cm,故AB=AG+BG.
解(1)过E作EF⊥AB,垂足为F.
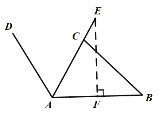
AE=AC+CE=58cm
在Rt△AEF中,∠CAB=60°,AE=58cm,
∴EF=AE·sin∠CAB=58sin60°=![]() cm.
cm.
答:车座点E到车架档AB的距离为![]()
(2)过C作CG⊥AB,垂足为G,
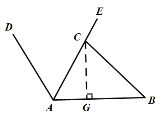
在Rt△ACG中,∠CAB=60°,AC=40cm,
则∠ACG=30°,∠BCG=∠ACB-∠ACG=45°
AG=AC·cos∠CAB=40cos60°=20cm
CG=AC·sin∠CAB=40sin60°=![]() cm
cm
在Rt△BCG中,∠BCG=45°,CG=![]() cm
cm
则BG=CG=![]() cm
cm
∴AB=AG+BG=(![]() )cm
)cm
答:车架档AB的长为![]() .
.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目