Question

【题目】如图，等边三角形中，是边的中点，是射线上一点，以为边作，使得，且，若，则的最小值为_______．

Answer 1

【答案】

【解析】

如下图，利用∠FEB=90°，可推导出△BED∽△EFG，设DE=x，根据和等边△ABC的边长为2，可得BD=1，GE=2，FG=2x，从而可用x表示出GA的长，在Rt△FGA中，利用勾股定理可求得用x表示的FA的长，最后利用二次函数性质，求得最小值

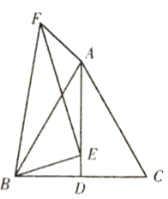
图下图，过点F作AD的垂线，交AD的方向延长线于点G．

∵∠BEF=90°

∴∠BED+∠FEG=90°

∵△ABC是正三角形，点D是BC中点，AB=2

∴∠BDA=90°，BD=1，AD=

∴∠EBD+∠BED=90°

∴∠EBD=∠FEG

∵∠BDE=∠FGE=90°

∴△BED∽△EFG

∵，∴

∴

∴EG=2

设DE=x，则AE=，GA=GE－AE=2+x－，FG=2x

∴在Rt△AFG中，

化简得：

要使AF最短，则只需要最小即可，即最小

令y=，则只需要求解二次函数的最小值即可

抛物线开口向上，顶点处即为最小值

此刻，，

∴结合二次函数的性质可得，

y=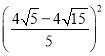

故AF的最小值为：

故答案为：