题目内容
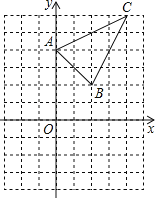
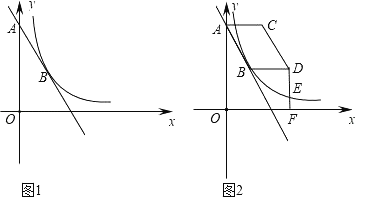
【题目】如图1,点A(0,8)、点B(2,a)在直线y=﹣2x+b上,反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
(1)求a和k的值;
(2)将线段AB向右平移m个单位长度(m>0),得到对应线段CD,连接AC、BD.
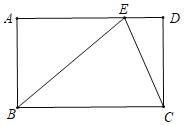
①如图2,当m=3时,过D作DF⊥x轴于点F,交反比例函数图象于点E,求E点的坐标;
②在线段AB运动过程中,连接BC,若△BCD是等腰三形,求所有满足条件的m的值.
【答案】(1)a=4,k=8;(2)①E(5,![]() );②满足条件的m的值为4或5或2
);②满足条件的m的值为4或5或2![]() .
.
【解析】
(1)把点A坐标代入直线AB的解析式中,求出a,求出点B坐标,再将点B坐标代入反比例函数解析式中求出k;
(2)①确定出点D(5,4),得到求出点E坐标;
②先表示出点C,D坐标,再分三种情况:当BC=CD时,判断出点B在AC的垂直平分线上,即可得出结论,当BC=BD时,表示出BC,用BC=BD建立方程求解即可得出结论,当BD=AB时,m=AB,根据勾股定理计算即可.
解:(1)∵点A(0,8)在直线y=﹣2x+b上,
∴﹣2×0+b=8,
∴b=8,
∴直线AB的解析式为y=﹣2x+8,
将点B(2,a)代入直线AB的解析式y=﹣2x+8中,得﹣2×2+8=a,
∴a=4,
∴B(2,4),
将B(2,4)代入反比例函数解析式y=![]() (x>0)中,得k=xy=2×4=8;
(x>0)中,得k=xy=2×4=8;
(2)①由(1)知,B(2,4),k=8,∴反比例函数解析式为y=![]() ,
,
当m=3时,将线段AB向右平移3个单位长度,得到对应线段CD,
∴D(2+3,4),即D(5,4),
∵DF⊥x轴于点F,交反比例函数y=![]() 的图象于点E,
的图象于点E,
∴E(5,![]() );
);
②如图,
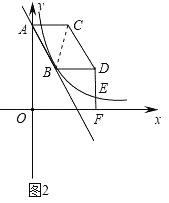
∵将线段AB向右平移m个单位长度(m>0),得到对应线段CD,
∴CD=AB,AC=BD=m,
∵A(0,8),B(2,4),
∴C(m,8),D((m+2,4),
△BCD是等腰三形,
当BC=CD时,BC=AB,
∴点B在线段AC的垂直平分线上,
∴m=2×2=4,
当BC=BD时,B(2,4),C(m,8),
∴![]() ,
,
∴![]() ,
,
∴m=5,
当BD=AB时,![]() ,
,
综上所述,△BCD是以BC为腰的等腰三角形,满足条件的m的值为4或5或2![]() .
.