题目内容
【题目】在一个箱子中有三个分别标有数字1，2，3的材质、大小都相同的小球，从中任意摸出一个小球，记下小球的数字x后，放回箱中并摇匀，再摸出一个小球，又记下小球的数字y。以先后记下的两个数字（x,y）作为点P的坐标。
（1）求点P的横坐标与纵坐标的和为4的概率，并画出树状图或列表；
（2）求点P落在以坐标原点为圆心、
为半径的圆的内部的概率。
【答案】（1）
．（2）
．
【解析】
试题分析：（1）首先根据题意列出表格，然后根据表格即可求得点M坐标的所有可能的结果，然后利用概率公式解即可；
（2）确定满足条件的点的个数，利用概率公式求解，即可求得答案．
试题解析：（1）列表得：
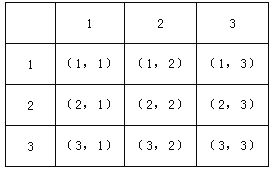
则点M坐标的所有可能的结果有九个：（1，1）、（1，2）、（1，3）、（2，1）、（2，2）、
（2，3）、（3，1）、（3，2）、（3，3），和为4的有3种，
故P（和为4）= 
=．
（2）因为点M在以坐标原点为圆心，以
为半径的圆的内部，
所以x2+y2＜10，这样的点M有4种形式：（1，1）、（1，2）、（2，1）、（2，2），
所以点M在以坐标原点为圆心，以为半径的圆的内部的概率P=．
练习册系列答案
相关题目
