题目内容
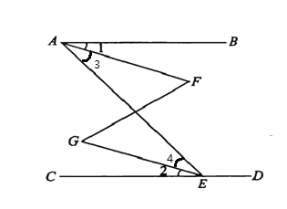
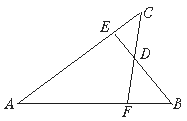
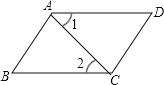
【题目】 根据题意，完成推理填空：如图，AB∥CD，∠1＝∠2，试说明∠B＝∠D．
解：∵∠1＝∠2（已知）
∴ （內错角相等，两直线平行）
∴∠BAD+∠B＝180°（两直线平行，同旁内角互补）
∵AB∥CD
∴ + ＝180°，
∴∠B＝∠D
【答案】AD∥BC；已知；∠B；∠BCD；两直线平行，同旁内角互补；等量代换．
【解析】
根据平行线的判定定理以及性质解答此题即可.
解：∵∠1＝∠2（已知）
∴AD∥BC（內错角相等，两直线平行）
∴∠BAD+∠B＝180°（两直线平行，同旁内角互补）
∵AB∥CD（已知）
∴∠B+∠BCD＝180°（两直线平行，同旁内角互补）
∴∠B＝∠D（等量代换）
故答案为：AD∥BC；已知；∠B；∠BCD；两直线平行，同旁内角互补；等量代换．
【题目】探究函数y=x+
（x＞0）与y=x+
（x＞0，a＞0）的相关性质．
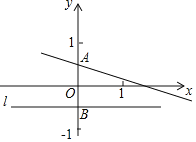
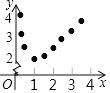
（1）小聪同学对函数y=x+（x＞0）进行了如下列表、描点，请你帮他完成连线的步骤；观察图象可得它的最小值为 ，它的另一条性质为 ；
x | … |
|
|
| 1 |
| 2 |
| 3 | … |
y | … |
|
|
| 2 |
|
|
|
| … |
（2）请用配方法求函数y=x+（x＞0）的最小值；
（3）猜想函数y=x+（x＞0，a＞0）的最小值为 ．
【题目】甲、乙两组同学进行一分钟引体向上测试，评分标准规定，做6个以上
含6个
为合格，做9个以上含9个为优秀，两组同学的测试成绩如下表：
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
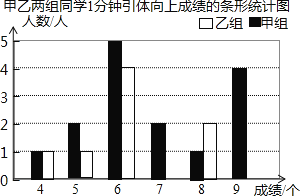
现将两组同学的测试成绩绘制成如下不完整的统计图表：
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
将条形统计图补充完整；
统计表中的
______，
______；
人说甲组的优秀率高于乙组优秀率，所以甲组成绩比乙组成绩好，但也有人说乙组成绩比甲组成绩好，请你给出两条支持乙组成绩好的理由．