题目内容
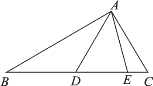
【题目】如图, 在△DAE中, ∠DAE=40°, B、C两点在直线DE上,且∠BAE=∠BEA,∠CAD=∠CDA,则∠BAC的大小是( )
A.100°B.90°C.80°D.120°
【答案】A
【解析】
由已知条件,利用了中垂线的性质得到线段相等及角相等,再结合三角形内角和定理求解.
解:

如图,∵BG是AE的中垂线,CF是AD的中垂线,
∴AB=BE,ACECD
∴∠AED=∠BAE=∠BAD+∠DAE,∠CDA=∠CAD=∠DAE+∠CAE,
∵∠DAE+∠ADE+∠AED=180°
∴∠BAD+∠DAE+∠DAE+∠CAE+∠DAE=3∠DAE+∠BAD+∠EAC=120°+∠BAD+ ∠EAC=180°
∴∠BAD+∠EAC=60°
∴. ∠BAC=∠BAD+∠EAC+∠DAE=60°+40°=100°;
故选:A

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目