Question

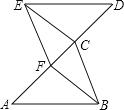
【题目】如图，已知∠BAE＋∠AED＝180°，∠1＝∠2，那么∠F＝∠G吗？为什么？

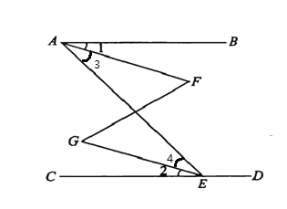
解：因为∠BAE＋∠AED＝180°( 已知)

所以AB∥CD________

所以∠BAE＝∠AEC________

因为∠1＝∠2( 已知)

所以∠BAE—∠1＝∠AEC—∠2(等式性质)

即∠3＝∠4

所以AF∥EG________，

所以∠F＝∠G________.

Answer 1

【答案】同旁内角互补，两直线平行；两直线平行，内错角相等；内错角相等，两直线平行；两直线平行，内错角相等．

【解析】

先根据题意得出AB∥CD，故可得出∠BAE=∠AEC，再由∠1=∠2得出∠FAE=∠GEA，进而可得出AF∥EG，据此可得出结论．

解：∵∠BAE+∠AED=180°（已知），∴AB∥CD（同旁内角互补，两直线平行），

∴∠BAE=∠AEC（两直线平行，内错角相等），

∵∠1=∠2（已知），∴∠BAE－∠1=∠AEC－∠2（等式性质），即∠3＝∠4，

∴AF∥EG（内错角相等，两直线平行），

∴∠F=∠G（两直线平行，内错角相等）．

故答案为：同旁内角互补，两直线平行；两直线平行，内错角相等；内错角相等，两直线平行；两直线平行，内错角相等．