题目内容
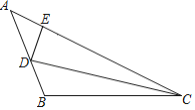
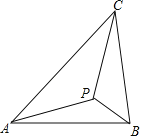
【题目】(1)如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1,P2是点P关于AB、AC的对称点,连结P1P2,分别交AB、AC于点D、E.
(1)若∠A=52°,求∠DPE的度数;
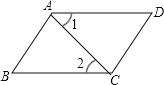
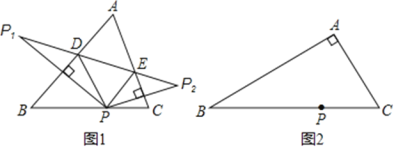
(2)如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2,(不写作法,保留作图痕迹),试判断点P1,P2与点A是否在同一直线上,并说明理由.
【答案】(1)∠DPE=76°;(2)详见解析.
【解析】
(1)利用轴对称的性质证明:∠DPP1+∠EPP2=∠A,根据∠DPE=180°-(∠PDE+∠DEF)计算即可;
(2)点P1,P2与点A在同一条直线上.证明∠PAP1+∠PAP2=180°即可.
解:(1)∵P1,P2是点P关于AB、AC的对称点,
∴PD=P1D,PE=P2E,
∴∠EDP=2∠DPP1,∠DEP=2∠EPP2,
∵∠DPP1+∠DPE+∠EPP2+∠A=180°①,
2∠DPP1+∠DPE+2∠EPP2=180°②
②-①得:∠DPP1+∠EPP2=∠A,
∵∠A=52°,
∴∠DPP1+∠EPP2=52°,
∴∠DPE=180°-(∠PDE+∠DEF)
=180°-2(∠DPP1+∠EPP2)
=180°-104°=76°.
(2)点P1,P2与点A在同一条直线上.
理由如下:连接AP,AP1,AP2.
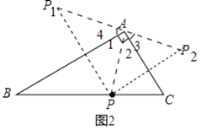
根据轴对称的性质,可得∠4=∠1,∠3=∠2,
∵∠BAC=90°,即∠1+∠2=90°,
∴∠3+∠4=90°,
∴∠1+∠2+∠3+∠4=180°,即∠P1AP2=180°,
∴点P1,P2与点A在同一条直线上.

练习册系列答案
相关题目