Question

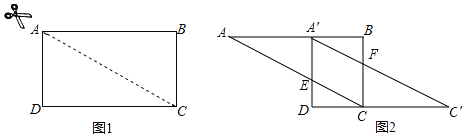
【题目】如图，正方形ABCD的边长为25，内部有6个全等的正方形，小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上，则每个小正方形的边长为_____．

Answer 1

【答案】

【解析】

如图，过点G作GP⊥AD，垂足为P，可以得到△BGF∽△PGE，再根据相似三角形对应边成比例的性质列式求解即可得到DE和BG，根据勾股定理可求EG的长，进而求出每个小正方形的边长．

解：如图所示：

∵正方形ABCD边长为25，

∴∠A=∠B=90°，AB=25，

过点G作GP⊥AD，垂足为P，则∠4=∠5=90°，

∴四边形APGB是矩形，

∴∠2+∠3=90°，PG=AB=25，

∵六个大小完全一样的小正方形如图放置在大正方形中，

∴∠1+∠2=90°，

∴∠1=∠FGB，

∴△BGF∽△PGE，

∴= ，

∴= ，

∴GB=5．

∴AP=5．

同理DE=5．

∴PE=AD﹣AP﹣DE=15，

∴EG==5，

∴小正方形的边长为．

故答案为：．