题目内容
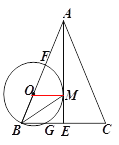
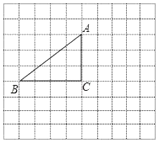
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、点B、点C均落在格点上
(Ⅰ)线段AB的长度=________;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,在∠ABC的平分线上找一点P,在BC上找一点Q,使CP+PQ的值最小,并简要说明点P,Q的位置是如何找到的_____________(不要求证明).
【答案】5 构造边长为5的菱形ABKD,连接BD,射线BD为∠ABC的平分线,构造△CEF≌△CAB,作直线CF交BD于P,交AB于Q′,再作点P关于直线BC的对称点J,连接PJ交BC于点Q,点P、Q即为所求;
【解析】
(Ⅰ)根据勾股定理计算即可;
(Ⅱ)构造边长为5的菱形ABKD, 得到射线BD为∠ABC的平分线,再构造△CEF≌△CAB,作直线CF交BD于P,交AB于Q′,再作点P关于直线BC的对称点J,连接PJ交BC于点Q,即可找到符合题意的点.
解:(Ⅰ)![]() ,
,
故答案为:5;
(Ⅱ)构造边长为5的菱形ABKD,连接BD,射线BD为∠ABC的平分线,构造△CEF≌△CAB,作直线CF交BD于P,交AB于Q′,再作点P关于直线BC的对称点J,连接PJ交BC于点Q,点P、Q即为所求.
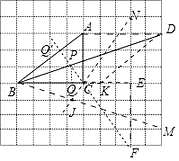
故答案为:构造边长为5的菱形ABKD,连接BD,射线BD为∠ABC的平分线,构造△CEF≌△CAB,作直线CF交BD于P,交AB于Q′,再作点P关于直线BC的对称点J,连接PJ交BC于点Q,点P、Q即为所求.

【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间(小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3
C. 平均数是3 D. 方差是0.34