题目内容
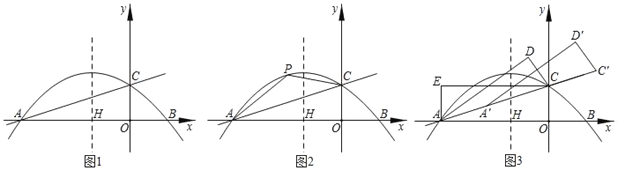
【题目】如图,抛物线![]() 与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.
与x轴分别相交于点A(﹣2,0),B(4,0),与y轴交于点C,顶点为点P.

(1)求抛物线的解析式;
(2)动点M、N从点O同时出发,都以每秒1个单位长度的速度分别在线段OB、OC上向点B、C方向运动,过点M作x轴的垂线交BC于点F,交抛物线于点H.
①当四边形OMHN为矩形时,求点H的坐标;
②是否存在这样的点F,使△PFB为直角三角形?若存在,求出点F的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)①H(
;(2)①H(![]() ,
,![]() );②存在,F的坐标为(
);②存在,F的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)把A和B的坐标代入抛物线解析式,即可求出b、c的值,从而得到抛物线的解析式;
(2)①表示出ON、MH,运用ON=MH,列方程求解即可;
②存在,先求出BC的解析式,根据互相垂直的直线一次项系数积等于﹣1,直线经过点P,用待定系数法求出直线PF的解析式,然后求直线BC与直线PF的交点坐标即可.
解:(1)把A(﹣2,0),B(4,0),代入抛物线![]() 得:
得:![]() ,解得:b=1,c=4,∴
,解得:b=1,c=4,∴![]() ;
;
(2)点C的坐标为(0,4),B(4,0),∴直线BC的解析式为![]() ,
,
①根据题意,ON=OM=t,MH=![]() ,∵ON∥MH,∴当ON=MH时,四边形OMHN为矩形,即
,∵ON∥MH,∴当ON=MH时,四边形OMHN为矩形,即![]() ,解得:
,解得:![]() 或
或![]() (不合题意舍去),把
(不合题意舍去),把![]() 代入
代入![]() 得:
得:![]() ,∴H(
,∴H(![]() ,
,![]() );
);
②存在,当PF⊥BC时,∵直线BC的解析式为![]() ,
,
∴设PF的解析式为![]() ,又点P(1,
,又点P(1,![]() )代入求得
)代入求得![]() ,
,
∴PF的解析式为![]() ,
,
∴根据题意列方程组: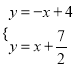 ,解得:
,解得: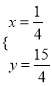 ,
,
∴F(![]() ,
,![]() );
);
当PF⊥BP时,∵点P(1,![]() ),B(4,0),
),B(4,0),
∴直线BP的解析式为:![]() ,
,
∴设PF的解析式为![]() ,又点P(1,
,又点P(1,![]() )代入求得
)代入求得![]() ,
,
∴PF的解析式为![]() ,
,
∴根据题意列方程组: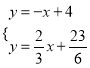 ,解得:
,解得: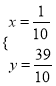 ,∴F(
,∴F(![]() ,
,![]() ),
),
综上所述:△PFB为直角三角形时,点F的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目