��Ŀ����
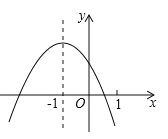
����Ŀ��![]() ��ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y����x+4��x�ύ�ڵ�A������A��������y��ax2+bx��ֱ��y����x+4������һ��B���ҵ�B�ĺ�����Ϊ1��
��ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬ֱ��y����x+4��x�ύ�ڵ�A������A��������y��ax2+bx��ֱ��y����x+4������һ��B���ҵ�B�ĺ�����Ϊ1��



��1���������ߵĽ���ʽΪ��
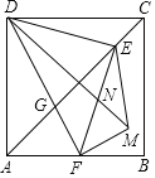
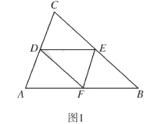
��2����ͼ1��QΪ��������λ��ֱ��AB�Ϸ���һ���㣨����B��A�غϣ�����Q��QP��x�ᣬ��x����P������AQ��MΪAQ�е㣬����PM����M��MN��PM��ֱ��AB��N������P�ĺ�����Ϊt����N�ĺ�����Ϊn����n��t�ĺ�����ϵʽ���ڴ������£���ͼ2������QN���ӳ�����y����E������AE����tΪ��ֵʱ��MN��AE��
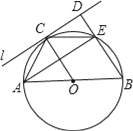
��3����ͼ3����ֱ��AB�Ƶ�A˳ʱ����ת15�Ƚ������߶Գ����ڵ�C����TΪ�߶�OA�ϵ�һ���㣨����O��A�غϣ����Ե�OΪԲ�ġ���OTΪ�뾶��Բ�����߶�OC���ڵ�D���Ե�AΪԲ�ġ���ATΪ�뾶��Բ�����߶�AC���ڵ�F������DF���ڵ�T�˶��Ĺ����У��ı���ODFA����������ֵ��������Сֵ���������ֵ��
���𰸡���1��y����x2+4x����2��n��![]() ����0��t��3���� t��2ʱ��MN��AE����3���ڵ�T�˶��Ĺ����У��ı���ODFA���������СֵΪ3
����0��t��3���� t��2ʱ��MN��AE����3���ڵ�T�˶��Ĺ����У��ı���ODFA���������СֵΪ3![]()
��������
��1���������A��B�����꣬Ȼ�����ô���ϵ������������������ߵĽ���ʽ��
��2������M��MG��x����G��NH��GM��H����֤��N��P��A��������MΪԲ��MAΪ�뾶�ġ�M�ϣ�Ȼ��õ���NMH�ա�MPG���õ�NH��MG��HM��PG������PΪ��t��0����Ȼ������t�ķ��̣��ⷽ�̼��ɵõ�t��ֵ��
��3����OT=m���ı���ODFA�����ΪS��CD��AF��AT��4��m��CF��OT��m����D��DR��AC������ΪR����DR��DCsin60����![]() ��4��m��������S��S��OAC��S��CDF���ɵó����ۣ�
��4��m��������S��S��OAC��S��CDF���ɵó����ۣ�
�⣺��1����ֱ��y����x+4��x�ύ�ڵ�A��
��y=0����x=4��
���A��4��0����
��ֱ��y����x+4������B����B�ĺ�����Ϊ1��
���B����������y����1+4=3��
���B����1��3����
�ѵ�A��B����y��ax2+bx����
![]() ����ã�
����ã�![]() ��
��
�������߽���ʽΪ![]() ��
��
��2����ͼ1������M��MG��x����G��NH��GM��H��
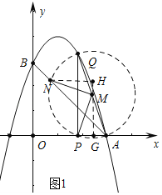
��OA��OB����AOB��90����
���PAN��45����
�ߡ�NMP��90����
���PAN��![]() ��NMP��
��NMP��
��N��P��A��������MΪԲ��MAΪ�뾶�ġ�M�ϣ�
��MN��MP��
�ߡ�NHM����PGM����NMP��90����
���NMH+��PMG��90������PMG+��MPG��90����
���NMH����MPG��
���NMH�ա�MPG��
��NH��MG��HM��PG��
��P��t��0����
��Q��t����t2+4t����M��![]() ��
��![]() ��
��
��MG��NH
��![]() ��n��
��n��![]()
��n��![]() ����0��t��3����
����0��t��3����
��MN��AE��QM��MA��
��EN��QN��
��NΪEQ�е㣬��Nx=![]()
��![]() ��
��![]() ��
��
��t2��4t+4��0��
��ã�t��2
��t��2ʱ��MN��AE��
��3���ı���ODFA���������Сֵ��
��OT��m���ı���ODFA�����ΪS
��C�������߶Գ���һ�㣬
��CO��CA��
��ֱ��AB��A����ת15����
���OAC=60��
���OAC�ǵȱ�������
��OA��4��S��OAC��![]() ��42��
��42��![]() ��
��
��CD��AF��AT��4��m��CF��OT��m��
��D��DR��AC������ΪR��
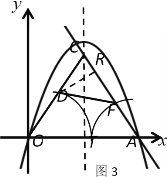
��DR��DCsin60����![]() ��4��m����
��4��m����
��S��CDF��![]() CFDR��
CFDR��![]() m
m![]() ��4��m������
��4��m������![]() m2+
m2+![]() m��
m��
��S��S��OAC��S��CDF
��4![]() ������
������![]() m2+
m2+![]() m��
m��
��![]() ��m��2��2+3
��m��2��2+3![]() ��
��
���ڵ�T�˶��Ĺ����У��ı���ODFA���������СֵΪ3![]() ��
��

 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�����Ŀ������ʦΪ���˽�ѧ�������ڼҵ��Ķ���������������20��ѧ��ijһ����Ķ�Сʱ�����������ͳ�����£�
�Ķ�ʱ�䣨Сʱ�� | 2 | 2.5 | 3 | 3.5 | 4 |
ѧ������������ | 1 | 2 | 8 | 6 | 3 |
�������20��ѧ���Ķ�Сʱ����˵����ȷ���ǣ� ��
A. ������8 B. �����3
C. ƽ������3 D. ������0.34