题目内容
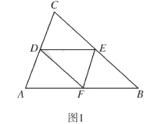
【题目】如图,在RtΔABC,∠C=90°,AC=4cm,BC=3cm,动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,MN,设移动时间为t(单位:秒,0<t<2.5).
(1)当t为何值时,ΔMCN面积为2cm?
(2)是否存在某一时刻t,使四边形APNC的面积为![]() cm?若存在,求t的值,若不存在,请说明理由;
cm?若存在,求t的值,若不存在,请说明理由;
(3)当t为何值时,以A、P、M为顶点的三角形与△ABC相似?

【答案】(1)2 (2)存在;1.5 (3)1.5
【解析】
(1)由题意可知CN=CM=t,再用含t的式子表示出三角形CMN的面积,再列方程即可求解;
(2)先根据勾股定理求出AB的长,过点P作PD⊥BC于点D,构造平行线PD∥AC,由平行线分线段成比例求得以t表示的PD的值,再根据“S四边形APNC=S△ABC-S△BPN”列出S与t的关系式,根据其面积等于![]() ,列方程求解,再将解进行检验即可得出结果.
,列方程求解,再将解进行检验即可得出结果.
(3)分类讨论:△AMP∽△ABC和△APM∽△ABC两种情况.利用相似三角形的对应边成比例来求t的值;
解:(1)由题意可知CN=CM=t,
∴S△MCN=![]() CMCN=
CMCN=![]() ,
,
∴![]() ,
,
解得t=2或t=﹣2(舍去),
∴当t的值为2时,△MCN的面积为2cm2;
(2)存在,理由如下:
如图1,过P作PD⊥BC于点D,则PD∥AC,
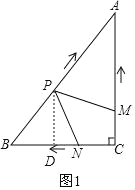
∴△PBD∽△ABC,
∴![]() ,
,
由题意可知AC=4cm,BC=3cm,
∴AB=5cm,且BP=2tcm,
∴![]() ,解得PD=
,解得PD=![]() cm,
cm,
∵CN=t,
∴BN=3﹣t,
∴S△PBN=![]() BNPD=
BNPD=![]() (3﹣t)×
(3﹣t)×![]() =
=![]() ,
,
∵S△ABC=![]() ACBC=
ACBC=![]() ×4×3=6,
×4×3=6,
∴S四边形APNC=S△ABC﹣S△PBN=6﹣(![]() )=
)=![]() ,
,
令S四边形APNC=![]() 可得
可得![]() =
=![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴当t=1.5时,四边形APNC的面积为![]() cm2;
cm2;
(3)由(2)可知AP=5﹣2t,AM=4﹣t,
∵△APM和△ABC中满足∠A=∠A,
∴由△APM和△ABC相似分两种情况,即△APM∽△ABC和△AMP∽△ABC,
当△APM∽△ABC时,则有![]() ,即
,即![]() ,解得t=0,不符合题意;
,解得t=0,不符合题意;
当△AMP∽△ABC时,则有![]() ,即
,即![]() ,解得t=1.5,
,解得t=1.5,
∴当t的值为1.5时,满足△APM和△ABC相似.