题目内容
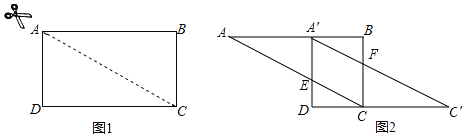
【题目】如图1,在矩形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 剪开,再把
剪开,再把![]() 沿
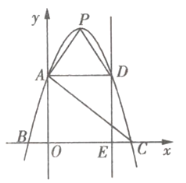
沿![]() 方向平移,得到图2,其中
方向平移,得到图2,其中![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() .
.
(1)在图2中,除![]() 与
与![]() 外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;
外,指出还有哪几对全等三角形(不能添加辅助线和字母),并选择一对加以证明;
(2)设![]() .①当
.①当![]() 为何值时,四边形
为何值时,四边形![]() 是菱形?②设四边形
是菱形?②设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ≌
≌![]() ,
,![]() ≌
≌![]() ;理由见解析;(2)①
;理由见解析;(2)①![]() ;②最大值为
;②最大值为![]() .
.
【解析】
(1)根据图形得到全等的三角形![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,利用ASA证明
,利用ASA证明![]() ≌
≌![]() ;
;
(2)①证明![]() ∽△ABC,求出
∽△ABC,求出![]() ,证明△
,证明△![]() ∽△BAC求出
∽△BAC求出![]() ,根据菱形的性质得到
,根据菱形的性质得到![]() ,即可求出x;
,即可求出x;
②证明四边形![]() 是平行四边形,利用面积公式求出面积y,再配方为顶点式即可得到y的最大值.
是平行四边形,利用面积公式求出面积y,再配方为顶点式即可得到y的最大值.
(1)![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,
,
证明∵图1中,![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ;
;
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() .
.
(2)①∵![]() ,
,![]() ,∠BAC=90°,
,∠BAC=90°,
∴AC=5,
∵![]() ∥BC,
∥BC,
∴![]() ∽△ABC,
∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ∥AC,
∥AC,
∴△![]() ∽△BAC,
∽△BAC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵四边形![]() 是菱形,
是菱形,
∴![]() ,
,
∴![]() ,
,
解得![]() ;
;
②∵AB∥![]() ,
,![]() ∥BC,
∥BC,
∴四边形![]() 是平行四边形
是平行四边形
∴![]()
![]()
∴y最大值为![]() .
.

练习册系列答案
相关题目