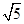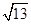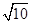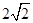题目内容
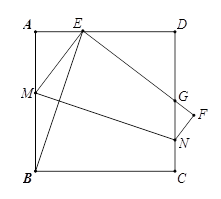
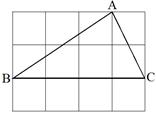
如图,在RtΔABC中,∠BAC=90°,DB⊥BC,DA=DB,点E是BC的中点,DE与AB相交于点G.
(1)求证DE⊥AB;
(2)如果∠FCB=∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.
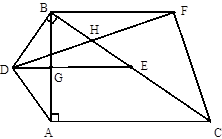
(1)求证DE⊥AB;
(2)如果∠FCB=∠FBC=∠DAB,设DF与BC交于点H,求证:DH=FH.
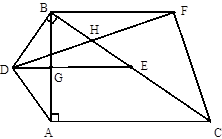
(1)证明见解析;(2)证明见解析.
试题分析:(1)欲证明DE⊥AB,只需推知AE=BE即可;
(2)欲证明DH=FH,需要证得四边形BDEF是平行四边形.
(1)如图,连接AE.
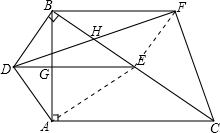
∵∠BAC=90°,BE=EC,
∴AE=BE=
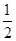 BC.
BC.又∵DA=DB,
∴DE垂直平分AB,即DE⊥AB;
(2)∵∠DBC=90°
∴∠DBA+∠ABC=90°
∵DA=AB,∴∠DBA=∠DAB,
∵∠FBC=∠DAB
∴∠FBC+∠ABC=90°
∵∠AGE=90°
∴BF∥DE.
又∵∠FBC=∠FCB,
∴FB=FC
∵BE=EC,∴FE⊥BC
∴∠DBE=∠BEF=90°
∴DB∥EF,
∴四边形DBFE是平行四边形,
∴DH=FH.

练习册系列答案
相关题目