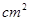题目内容
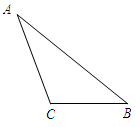
如图,在△ABC中,已知∠B=∠C
(1)尺规作图:作底角∠ABC的平分线BD,交AC于点D(作图不写作法,但保留作图痕迹);
(2)猜想:“若∠A=36°,则△ABD和△BDC都是等腰三角形”。请你通过计算说明猜想是否成立.

(1)尺规作图:作底角∠ABC的平分线BD,交AC于点D(作图不写作法,但保留作图痕迹);
(2)猜想:“若∠A=36°,则△ABD和△BDC都是等腰三角形”。请你通过计算说明猜想是否成立.

(1)作图见解析;(2)理由见解析.
试题分析:(1)首先以B为圆心,任意长为半径画弧,两弧交AB、BC于M、N两点;再分别以M、N为圆心,大于
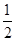 MN长为半径画弧,两弧交于一点O,画射线BO交AC于D.
MN长为半径画弧,两弧交于一点O,画射线BO交AC于D.(2)根据三角形内角和为180°计算出∠ABC,∠C,∠CDB,∠ABD,∠DBC的度数,再根据等角对等边可证出结论.
试题解析:(1)如图所示:
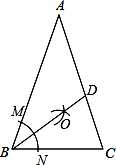
BD即为所求;
(2)∵∠A=36°,
∴∠ABC=∠C=(180°-36°)÷2=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=72°÷2=36°,
∴∠CDB=180°-36°-72°=72°,
∵∠A=∠ABD=36°,∠C=∠CDB=72°,
∴AD=DB,BD=BC,
∴△ABD和△BDC都是等腰三角形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
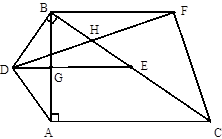
 ABCD中,点E、F在BD上,且BF=DE.
ABCD中,点E、F在BD上,且BF=DE.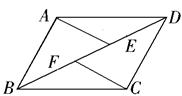
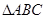 的三边长分别是6cm、8cm、10cm,则
的三边长分别是6cm、8cm、10cm,则