题目内容
如图，M、N是正方形ABCD边AB、CD上两动点，连接MN，将四边形BCNM沿MN折叠，使点B落在AD边上点E处、点C落在点F.
（1）求证：BE平分∠AEF；
（2）求证：C△EDG=2AB（注：C△EDG表示△EDG的周长）
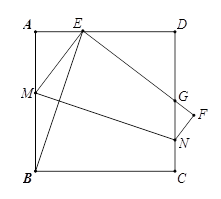
（1）求证：BE平分∠AEF；
（2）求证：C△EDG=2AB（注：C△EDG表示△EDG的周长）
（1）证明见解析；（2）证明见解析.
试题分析：（1）根据折叠和正方形的性质即可证明.
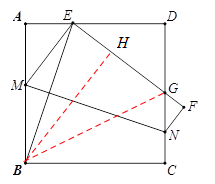
（2）过点B作BH垂直EF，垂足为H，连接BG，由△BAE≌△BHE和△BHG≌△BCG即可证得AE＝EH，HG＝CG，从而ED+DG+EG ＝ED+DG+AE+CG＝AD+CD＝2AB.
（1）∵四边形BCNM沿MN折叠，∴BM=EM，∠MEF=∠MBC=900.
∴∠MBE=∠MEB.∴∠BEF=900-∠MEB.
∵∠A=900，∴∠AEB=900-∠MBE.
∴∠AEB=∠BEF.
（2）如图，过点B作BH垂直EF，垂足为H，连接BG .
易证△BAE≌△BHE，△BHG≌△BCG，
∴AE＝EH，HG＝CG .
又∵ED+DG+EG＝ED+DG+EH+HG，
∴ED+DG+EG ＝ED+DG+AE+CG＝AD+CD＝2AB.
练习册系列答案
名校课堂系列答案
相关题目
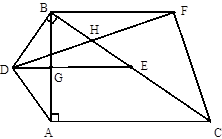
BD；其中正确结论的是（ ）
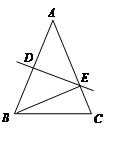
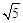，0），B（
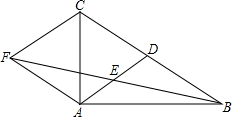
ABCD中，点E、F在BD上，且BF＝DE．