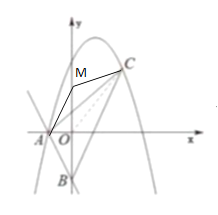题目内容
【题目】一次函数y=﹣2x﹣2分别与x轴、y轴交于点A、B.顶点为(1,4)的抛物线经过点A.
(1)求抛物线的解析式;
(2)点C为第一象限抛物线上一动点.设点C的横坐标为m,△ABC的面积为S.当m为何值时,S的值最大,并求S的最大值;
(3)在(2)的结论下,若点M在y轴上,△ACM为直角三角形,请直接写出点M的坐标.
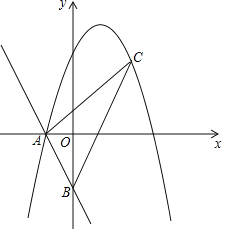
【答案】(1)y=﹣x2+2x+3
(2)当m=2时,S的值最大,最大值为![]()
(3)(0,﹣1)、(0,5)、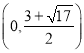 或
或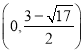
【解析】
(1)设抛物线的解析式为![]() ,代入点A的坐标即可求解.
,代入点A的坐标即可求解.
(2)连接0C,可得点![]() 根据一次函数y=-2x-2得出点A、B的坐标,然后利用三角形面积公式得出
根据一次函数y=-2x-2得出点A、B的坐标,然后利用三角形面积公式得出![]() 的表达式,利用二次函数的表达式即可求解.
的表达式,利用二次函数的表达式即可求解.
(3)设M(0,n),已知A、C点坐标可求出直线AC的解析式,分三种情况,当AC⊥MC,求出M点坐标,当AC⊥AM时,求出M点坐标,当AM⊥MC时,求出M点坐标.
(1)一次函数y=﹣2x﹣2与x轴交于点A,则A的坐标为(﹣1,0),
∵抛物线的顶点为(1,4),
∴设抛物线解析式为y=a(x﹣1)2+4,
∵抛物线经过点A(﹣1,0),
∴0=a(﹣1﹣1)2+4,
∴a=﹣1,
∴抛物线解析式为y=﹣(x﹣1)2+4=﹣x2+2x+3;
(2)连接OC,点C为第一象限抛物线上一动点,点C的横坐标为m,
∴C(m,﹣m2+2m+3),
一次函数y=﹣2x﹣2与y轴交于点B,则OB=2,
∵A的坐标为(﹣1,0),
∴OA=1,
∴![]() ,
,![]()
![]()
![]()
∴当m=2时,S的值最大,最大值为![]() .
.
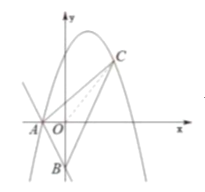
(3)设M(0,n),
∵A(﹣1,0),C(2,3),
∴直线AC的解析式为y=x+1,
①当AC⊥MC时,![]() =﹣1,
=﹣1,
∴n=5,
∴M(0,5);
②当AC⊥AM时,n=﹣1,
∴M(0,﹣1);
③当AM⊥MC时,![]() n=﹣1,
n=﹣1,
∴n=![]()
∴M(0,![]() )或M(0,
)或M(0,![]() );
);
综上所述:点M的坐标为(0,﹣1)、(0,5)、(0,![]() )或(0,
)或(0,![]() ).
).