题目内容
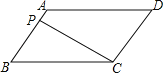
【题目】如图,ABCD中,AB=2,BC=4,∠B=60°,点P是四边形上的一个动点,则当△PBC为直角三角形时,BP的长为_____.
【答案】2或2![]() 或
或![]() .
.
【解析】
分两种情况:(1)①当∠BPC=90°时,作AM⊥BC于M,求出BM=![]() AB=1,AM=
AB=1,AM=![]() BM=
BM=![]() ,由勾股定理求出AC,由勾股定理的逆定理证出△ABC是直角三角形,∠BAC=90°,得出点P与A重合即可;②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,由勾股定理求出BP即可;
,由勾股定理求出AC,由勾股定理的逆定理证出△ABC是直角三角形,∠BAC=90°,得出点P与A重合即可;②当∠BPC=90°,点P在边AD上,CP=CD=AB=2时,由勾股定理求出BP即可;
(2)当∠BCP=90°时,CP=AM=![]() ,由勾股定理求出BP即可.
,由勾股定理求出BP即可.
解:分两种情况:
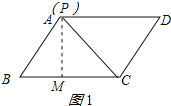
(1)①当∠BPC=90°时,
作AM⊥BC于M,如图1所示,
∵∠B=60°,
∴∠BAM=30°,
∴BM=![]() AB=1,
AB=1,
∴AM=![]() BM=
BM=![]() ,CM=BC﹣BM=4﹣1=3,
,CM=BC﹣BM=4﹣1=3,
∴AC=![]() =2
=2![]() ,
,
∴AB2+AC2=BC2,
∴△ABC是直角三角形,∠BAC=90°,
∴当点P与A重合时,∠BPC=∠BAC=90°,
∴BP=BA=2;
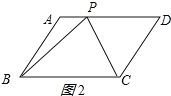
②当∠BPC=90°,
点P在边AD上,CP=CD=AB=2时,
BP=![]() =
=![]() =2
=2![]() ;
;
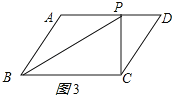
(2)当∠BCP=90°时,如图3所示:
则CP=AM=![]() ,
,
∴BP=![]() =
=![]() ;
;
综上所述:当△PBC为直角三角形时,BP的长为2或2![]() 或
或![]() .
.
故答案为:2或2![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目