Question

【题目】如图，在直角坐标系中，A，B为定点，A（2，﹣3），B（4，﹣3），定直线l∥AB，P是l上一动点，l到AB的距离为6，M，N分别为PA，PB的中点下列说法中：

①线段MN的长始终为1；②△PAB的周长固定不变；

③△PMN的面积固定不变； ④若存在点Q使得四边形APBQ是平行四边形，则Q到MN所在直线的距离必为9．

其中正确的说法是_____．

Answer 1

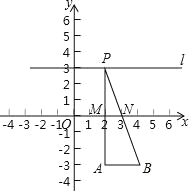
【答案】①③④

【解析】

根据三角形中位线打脸了判断①；根据三角形的周长公式判断②；根据相似三角形的性质定理判断③，根据平行四边形的性质判断④．

∵点A的坐标为（2，﹣3），点B的坐标（4，﹣3），

∴AB＝2，

∵M，N分别为PA，PB的中点，

∴MN＝AB＝1，①正确；

当点P在直线l上运动时，PA、PB发生变化，

∴△PAB的周长是变化的，②错误；

S△ABC＝×2×6＝6，

∵M，N分别为PA，PB的中点，

∴MN∥AB，

∴△PMN∽△PAB，

∴＝，

∴△PMN的面积固定不变，③正确；

当四边形APBQ是平行四边形时，点Q到直线l的距离为12，

∵直线l到MN所在直线的距离为3，

∴Q到MN所在直线的距离为9，④正确；

故答案为：①③④．