Question

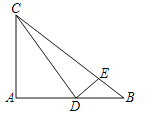
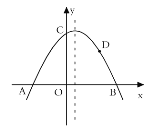
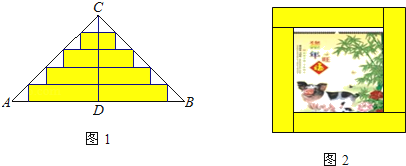
【题目】如图1，△ABC是一张等腰直角三角形彩色纸，AC＝BC，将斜边上的高CD五等分，然后裁出4张宽度相等的长方形纸条．若用这4张纸条刚好可以为一幅正方形美术作品镶边（纸条不重叠），如图2，则正方形美术作品与镶边后的作品的面积之比为_____．

Answer 1

【答案】4：9

【解析】

由图1中的△ABC是等腰直角三角形、AC＝AB，裁出的4张长方形纸宽度相同可知：图中△CEF∽△CGH∽△CIJ∽△CKL∽△CAB，且高CD把每张纸条左右平分，设AC＝BC＝a，则AB＝, CD＝，根据题意可得纸条的宽度为，根据相似三角形的性质可得EF、GH、IJ、KL，进而可得纸条总长度，据此可知，镶边后的作品的正方形的边长、正方形美术作品的边长，最后根据正方形的面积公式即可解答．

解：∵△ABC是等腰直角三角形，设AC＝BC＝a，如图所示：

∴AB＝＝＝，

∵CD是斜边上的高，

∴CD＝，

∵将斜边上的高CD五等分，

∴纸条的宽度为：，

由题意可知：△CEF∽△CGH∽△CIJ∽△CKL∽△CAB且＝，

∴EF＝，

同理，GH＝，

IJ＝，

KL＝，

∴纸条的总长度为：，

∴镶边后的作品的正方形的边长为：+＝，

∴面积为，

∵正方形美术作品的边长＝﹣＝，

∴面积为，

则正方形美术作品与镶边后的作品的面积之比为：4：9，

故答案为：4：9．