Question

【题目】如图，在矩形ABCD中，AB=，AD=3，点E从点B出发，沿BC边运动到点C，连结DE，点E作DE的垂线交AB于点F．在点E的运动过程中，以EF为边，在EF上方作等边△EFG，则边EG的中点H所经过的路径长是（　　）

A. 2 B. 3 C. D.

Answer 1

【答案】C

【解析】

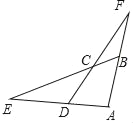
连接FH，取EF的中点M，连接BM，HM，据BM=EM=HM=FM,可得点B，E，H，F四点共圆，连接BH，则，进而得到点H在以点B为端点，BC上方且与射线BC夹角为30°的射线上，再过C作于点H'，根据点E从点B出发，沿BC边运动到点C，即可得到点H从点B沿BH运动到点H'，再利用在中，即可得出点H所经过的路径长是．

连接FH，取EF的中点M，连接BM，HM，

在等边三角形EFG中，EF=FG，H是EG的中点，

∴

又∵M是EF的中点，

∴FM=HM=EM，

在Rt△FBE中, M是EF的中点，

∴BM=EM=FM，

∴BM=EM=HM=FM,

∴点B，E，H，F四点共圆，

连接BH,则

∴点H在以点B为端点,BC上方且与射线BC夹角为的射线上，

如图，过C作CH′⊥BH于点H′，

∵点E从点B出发，沿BC边运动到点C，

∴点H从点B沿BH运动到点H′，

在Rt△BH′C中,

∴

∴点H所经过的路径长是.

故选:C.