题目内容
【题目】如图，已知
和
均为等腰三角形，
，
，将这两个三角形放置在一起．
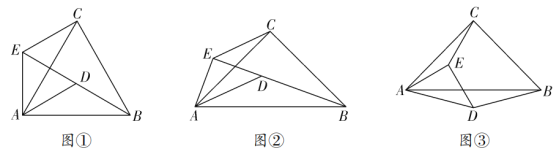
（1）问题发现
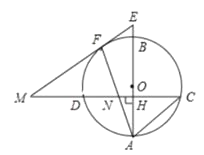
如图①，当
时，点
、
、
在同一直线上，连接
，则
的度数为__________，线段
、
、之间的数量关系是__________；
（2）拓展探究
如图②，当
时，点、、在同一直线上，连接．请判断的度数及线段、、之间的数量关系，并说明理由；
（3）解决问题
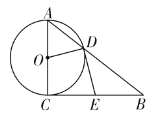
如图③，，
，
，连接、
，在
绕点
旋转的过程中，当
时，请直接写出
的长
【答案】（1）
；（2）
；（3）
或
．
【解析】
（1）证明△ACE≌△ABD，得出CE=AD，∠AEC=∠ADB，即可得出结论；（2）证明△ACE∽△ABD，得出∠AEC=∠ADB，
，即可得出结论；（3）先判断出，再求出
，①当点E在点D上方时，先判断出四边形APDE是矩形，求出AP=DP=AE=2，再根据勾股定理求出，BP=6，得出BD=4；②当点E在点D下方时，同①的方法得，AP=DP=AE=1，BP=4，进而得出BD=BP+DP=8，即可得出结论．
（1）在△ABC为等腰三角形，AC=BC，∠ACB=60°，
∴△ABC是等边三角形，
∴AC=AB，∠CAB=60°，
同理：AE=AD，∠ADE=∠EAD=60°，
∴∠EAD=∠CAB，
∴∠EAC=∠DAB，
∴△ACE≌△ABD（SAS），
∴CE=AD，∠AEC=∠ADB，
∵点B、D、E在同一直线上，
∴∠ADB=180°-∠ADE=120°，
∴∠AEC=120°，
∴
∵DE=AE，
∴BE=DE+BD=AE+CE，
故答案为60°，BE=AE+CE；
（2）．
理由如下：
和
均为等腰三角形， 
，
，
，
，
，
点
、
、
在同一直线上，
，
．
；
（3）由（2）知，△ACE∽△ABD，
∴，
在Rt△ABC中，
，
∴
；
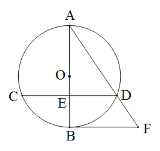
①当点E在点D上方时，如图③，过点A作AP⊥BD交BD的延长线于P，
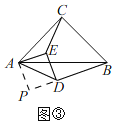
∵DE⊥BD，
∴∠PDE=∠AED=∠APD，
∴四边形APDE是矩形，
∵AE=DE，
∴矩形APDE是正方形，
∴AP=DP=AE=2，
在Rt△APB中，根据勾股定理得， 
∴BD=BP-AP=4，
∴
；
②当点E在点D下方时，如图④，
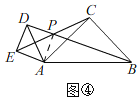
同①的方法得，AP=DP=AE=2，BP=4，
∴BD=BP+DP=8，
∴
，
即：CE的长为或．
