题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
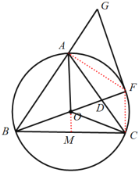
是![]() 的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与
的外接圆,连结OA、OB、OC,延长BO与AC交于点D,与![]() 交于点F,延长BA到点G,使得
交于点F,延长BA到点G,使得![]() ,连接FG.
,连接FG.
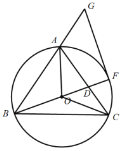
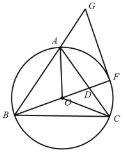
备用图
(1)求证:FG是![]() 的切线;
的切线;
(2)若![]() 的半径为4.
的半径为4.
①当![]() ,求AD的长度;
,求AD的长度;
②当![]() 是直角三角形时,求
是直角三角形时,求![]() 的面积.
的面积.
【答案】(1)见解析;(2)①![]() ,②当
,②当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)连接AF,由圆周角定理的推论可知![]() ,根据等腰三角形的性质及圆周角定理的推论可证
,根据等腰三角形的性质及圆周角定理的推论可证![]() ,
,![]() ,从而可得
,从而可得![]() ,然后根据切线的判定方法解答即可;
,然后根据切线的判定方法解答即可;
(2)①连接CF,根据“SSS”证明![]() ,由全等三角形及等腰三角形的性质可得
,由全等三角形及等腰三角形的性质可得![]() ,进而可证
,进而可证![]() ,由平行线分线段成比例定理可证
,由平行线分线段成比例定理可证![]() ,可求
,可求![]() ,然后由相交弦定理求解即可;
,然后由相交弦定理求解即可;
②分两种情况求解即可,(i)当![]() 时,(ii)当
时,(ii)当![]() 时.
时.
(1)连接AF,
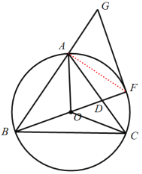
∵BF为![]() 的直径,
的直径,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
又∵OF为半径,
∴FG是![]() 的切线.
的切线.
(2)①连接CF,
则![]() ,
,
∵AB=AC,OB=OC,OA=OA,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∵半径是4,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
又由相交弦定理可得:![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() (舍负);
(舍负);
(2)②∵![]() 为直角三角形,
为直角三角形,![]() 不可能等于
不可能等于![]() .
.
∴(i)当![]() 时,则
时,则![]() ,
,
由于![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(ii)当![]() 时,
时,
∵![]() ,∴
,∴![]() 是等腰直角三角形,∴
是等腰直角三角形,∴![]() ,
,
延长AO交BC于点M,
∵AB=AC,
∴弧AB=弧AC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目