题目内容
如图是二次函数y=ax2+bx+c图像的一部分,其对称轴是直线x=-1,且过点(-3,0),下列说法:①abc>0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),(2.5,y2)是抛物在线两点,则y1>y2,其中正确的是( )
| A.② | B.②③ | C.②④ | D.①② |
C.
解析试题分析:∵二次函数的图象开口向上,
∴a>0,
∵二次函数的图象交y轴的负半轴于一点,
∴c<0,
∵对称轴是中线x=-1,
∴-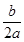 =-1,
=-1,
∴b=2a>0,
∴abc<0,
∴①错误;
∵b=2a,
∴2a-b=0,
∴②正确;
把x=2代入y=ax2+bx+c得:y=4a+2b+c,
从图象可知,当x=2时y<0,
即4a+2b+c<0,
∴③错误;
∵(-5,y1)关于直线x=-1的对称点的坐标是(3,y1),
又∵当x>-1时,y随x的增大而增大,3<5,
∴y1>y2,
∴④正确;
即正确的有2个②④.
故选:C.
考点: 二次函数图象与系数的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数是二次函数的是( )
A.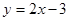 | B.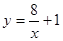 | C. | D. |
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0;②abc>0;③a-b+c>0;④2a-3b=0;⑤c-4b>0,你认为其中正确信息的个数有( )
| A.2个 | B.3个 | C.4个 | D.5个 |
将抛物线 向左平移2个单位,再向下平移3个单位,得到的抛物线是( )
向左平移2个单位,再向下平移3个单位,得到的抛物线是( )
A.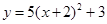 | B.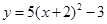 |
C.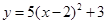 | D.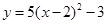 |
如图:点P(x,y)为平面直角坐标系内一点,PB⊥x 轴,垂足为B, A为(0,2),若PA=PB,则以下结论正确的是( ).
A.点P在直线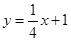 上 上 | B.点P在抛物线 上 上 |
C.点P在抛物线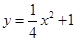 上 上 | D.点P在抛物线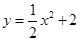 上 上 |
已知二次函数y=ax2+bx+c(a<0)的图象如图所示,当-5≤x≤0时,下列说法正确的是( )
| A.有最小值-5、最大值0 |
| B.有最小值-3、最大值6 |
| C.有最小值0、最大值6 |
| D.有最小值2、最大值6 |
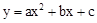 的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
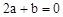
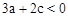

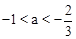
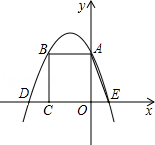
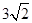 ,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是
,且这两个交点与抛物线的顶点是抛物线的内接格点三角形的三个顶点,则满足上述条件且对称轴平行于y轴的抛物线条数是