��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У��� A����2��0����B��2��0����C��0��2������ D����E�ֱ��� AC��BC���е㣬����CDE�Ƶ�C��ʱ����ת�õ���CD��E��������ת��Ϊ�������� AD����BE����
��1����ͼ������ 0��������90������ AD���CE��ʱ�������Ĵ�С��
��2����ͼ������ 90��������180�������� D�������߶� BE����ʱ���� sin��CBE����ֵ��
��3����ֱ��AD����ֱ��BE���ཻ�ڵ�P�����P�ĺ�����m��ȡֵ��Χ��ֱ��д�������������

���𰸡���1��60�㣻��2��![]() ����3����
����3����![]() ��m��
��m��![]() ��
��
�����������������(1)��ͼ1�У�����ƽ���ߵ����ʿɵá�AD��C=��E��CD��=90�㣬�ٸ���AC=2CD�䣬�Ƴ���CAD��=30�㣬�ɴ˼��ɽ�������� (2)��ͼ2�У���CK��BE����K�����ݹ��ɶ����͵���ֱ�������ε��������CK�ij����ٸ���sin��CBE��= ![]() �����ɽ��������(3)����ͼ3��ͼ4�ֱ������P����������ֵ�Լ���Сֵ���ɽ������.
�����ɽ��������(3)����ͼ3��ͼ4�ֱ������P����������ֵ�Լ���Сֵ���ɽ������.
���������
��1����ͼ1�У�
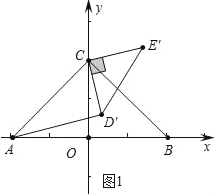
��AD���CE�䣬
���AD��C=��E��CD��=90�㣬
��AC=2CD�䣬
���CAD��=30�㣬
���ACD��=90�㩁��CAD��=60�㣬
���=60�㣮
��2����ͼ2�У���CK��BE����K��
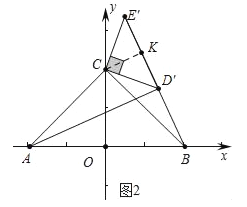
��AC=BC= ![]() =2
=2 ![]() ��
��
��CD��=CE��= ![]() ��
��
�ߡ�CD��E���ǵ���ֱ�������Σ�CD��=CE��= ![]() ��
��
��D��E��=2��
��CK��D��E�䣬
��KD��=E��K��
��CK= ![]() D��E��=1��
D��E��=1��
��sin��CBE��= ![]() =
= ![]() =
= ![]() ��
��
��3����ͼ3�У���CΪԲ��![]() Ϊ�뾶����C����BE�����C����ʱAP������ı���CD��PE���������Σ���PH��AB��H��
Ϊ�뾶����C����BE�����C����ʱAP������ı���CD��PE���������Σ���PH��AB��H��
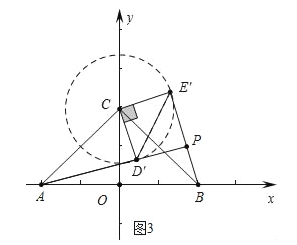
��AP=AD��+PD��= ![]() +
+ ![]() ��
��
��cos��PAB= ![]() =
= ![]() ��
��
��AH=2+ ![]() ��
��
���P����������ֵΪ![]() ��
��
��ͼ4�У���BE�����C����ʱAP��̣����ı���CD��PE���������Σ���PH��AB��H��
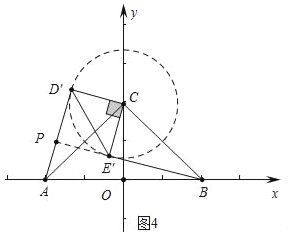
���ݶԳ��Կ�֪OH= ![]() ��
��
���P���������СֵΪ��![]() ��
��
���P�������ȡֵ��ΧΪ��![]() ��m��
��m��![]() ��
��

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�



