题目内容
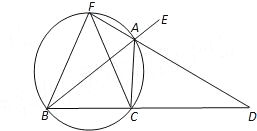
【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
(1)求证:FB=FC;
(2)求证:FB2=FAFD;
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)根据角平分线的性质,得两角相等,然后根据园内接四边形得到四边形的一个外角等于不相邻的一个内角,得到两个角相等,根据同弧所对的圆周角相等和对顶角相等,得到∠FBC=∠ACB,进而根据等角对等边得证;
(2)根据两个三角形对应角相等,得到两三角形相似,根据相似三角形的对应边相等得到对应边成比例,从而得到乘积式得证.
试题解析:(Ⅰ)∵AD平分∠EAC,
∴∠EAD=∠DAC.
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC.
∵∠EAD=∠FAB=∠FCB,
∴∠FBC=∠FCB,
∴FB=FC.
(Ⅱ)∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD,
∴△FBA∽△FDB
∴![]() ,
,
∴FB2=FAFD.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目